Vrijeme: 17:59
Dođite na MBL | Come to MBL #4
Neka je  unija poligona u trodimenzionalnom prostoru. Znamo da je projekcija
unija poligona u trodimenzionalnom prostoru. Znamo da je projekcija  na svaku od ravnina
na svaku od ravnina 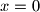 ,
, 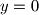 i
i 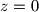 kvadrat stranice duljine 1.
kvadrat stranice duljine 1.
 unija poligona u trodimenzionalnom prostoru. Znamo da je projekcija
unija poligona u trodimenzionalnom prostoru. Znamo da je projekcija  na svaku od ravnina
na svaku od ravnina 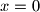 ,
, 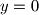 i
i 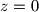 kvadrat stranice duljine 1.
kvadrat stranice duljine 1.Odredite najmanju moguću površinu od  .
.
NAPOMENA: Ovaj je zadatak bio dio MBL QQ 2023.
Let  be a union of polygons sitting inside three dimensional space. We know that the projection of
be a union of polygons sitting inside three dimensional space. We know that the projection of  onto each of the three planes
onto each of the three planes 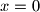 ,
, 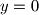 and
and 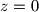 is a square with side length 1.
is a square with side length 1.
 be a union of polygons sitting inside three dimensional space. We know that the projection of
be a union of polygons sitting inside three dimensional space. We know that the projection of  onto each of the three planes
onto each of the three planes 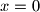 ,
, 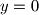 and
and 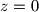 is a square with side length 1.
is a square with side length 1.What is the minimal possible area of  ?
?
NOTE: This problem was a part of MBL QQ 2023.
