Na večeri, Matej mora skenirati akreditaciju svakog učenika kako bi se organizatori "uvjerili da je živ". Akreditacija svake osobe je jedinstvena.
Matej skenira akreditaciju svake osobe koja prođe kroz vrata, uključujući učenike, predavače i organizatore, i prestaje kada skenira sve učenike (ali možda neće skenirati sve organizatore i predavače).
Ako je poznato da je na kampu sudjelovalo 60 učenika, 10 predavača i 8 organizatora, na koliko različitih načina je Matej mogao skenirati osobe na kampu, a da se na kraju uvjerio da su svi učenici živi? Kako se radi o velikom broju, odredi njegov ostatak pri dijeljenju s 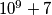 .
.
In the evening, Matej has to scan the credentials of each student so that the organizers can "make sure that he is alive". Each person's accreditation is unique.
Matej scans the credentials of every person who walks through the door, including students, lecturers and organizers, and stops when it scans all students (but may not scan all organizers and lecturers).
If it is known that 60 students, 10 lecturers and 8 organizers participated in the camp, in how many different ways could Matej scan the people at the camp, and in the end make sure that all the students are alive? Since it is a large number, determine its remainder when divided by 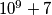 .
.
[lang = hr]
Na večeri, Matej mora skenirati akreditaciju svakog učenika kako bi se organizatori "uvjerili da je živ". Akreditacija svake osobe je jedinstvena.
Matej skenira akreditaciju svake osobe koja prođe kroz vrata, uključujući učenike, predavače i organizatore, i prestaje kada skenira sve učenike (ali možda neće skenirati sve organizatore i predavače).
Ako je poznato da je na kampu sudjelovalo 60 učenika, 10 predavača i 8 organizatora, na koliko različitih načina je Matej mogao skenirati osobe na kampu, a da se na kraju uvjerio da su svi učenici živi?
Kako se radi o velikom broju, odredi njegov ostatak pri dijeljenju s $10^9+7$.
[/lang]
[lang = en]
In the evening, Matej has to scan the credentials of each student so that the organizers can "make sure that he is alive". Each person's accreditation is unique.
Matej scans the credentials of every person who walks through the door, including students, lecturers and organizers, and stops when it scans all students (but may not scan all organizers and lecturers).
If it is known that 60 students, 10 lecturers and 8 organizers participated in the camp, in how many different ways could Matej scan the people at the camp, and in the end make sure that all the students are alive?
Since it is a large number, determine its remainder when divided by $10^9+7$.
[/lang]
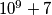 .
. 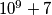 .
. 