Namješten 37 | Overfitting 37 #1
Matej i Patricija piju kavu i pričaju o svojim omiljenim funkcijama. Matej posebno voli polinome. No, Patricija nije toliko basic, pa zato želi da Matej pogodi njenu omiljenu funkciju, i to konkretno njenu vrijednost u 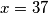 , najsavršenijem prostom broju.
, najsavršenijem prostom broju.
Patricija je Mateju otkrila da je 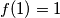 i
i  .
.
Ako Matej pretpostavi da je Patricijina funkcija oblika 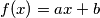 za neke realne brojeve
za neke realne brojeve  i
i  , koliko bi tada iznosio
, koliko bi tada iznosio 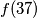 ?
?
Matej and Patricija are drinking coffee and talking about their favorite functions. Matej especially likes polynomials. But Patricija is not that basic, so she wants Matej to guess her favorite function, specifically its value in 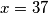 , the most perfect prime number.
, the most perfect prime number.
Patricija revealed to Matej that 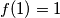 and
and  .
.
If Matej assumes that Patricija's function is of the form 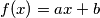 for some real numbers
for some real numbers  and
and  , what would be the value of
, what would be the value of 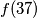 ?
?
