Vrijeme: 18:00
Vjerojatno lanac iz kinematike | Probably from kinematics #4
U prvom kvadrantu koordinatnog sustava se nalazi dvodimenzionalnog spremnik horizontalne duljine 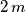 i visine
i visine 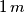 u donjem lijevom kutu spremnika(neka se donji lijevi kut nalazi u točki
u donjem lijevom kutu spremnika(neka se donji lijevi kut nalazi u točki 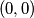 ) nalazi se
) nalazi se  jako malenih čestica od kojih svaka u trenutku
jako malenih čestica od kojih svaka u trenutku 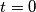 ima nasumičan vektor smjera određen preko nasumično odabrane točke iz ravnine i točke
ima nasumičan vektor smjera određen preko nasumično odabrane točke iz ravnine i točke 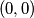 tako da je brzina iz
tako da je brzina iz ![[0,4] \, ms^{-1}](/media/m/c/5/b/c5b1d368916bceecdc716f53b6d9cf0b.png) i kut između
i kut između ![[0,\frac{\pi} {2}]](/media/m/c/4/4/c444f378dc333f50e2dba634ad695486.png) .
.
Spremnik je podijeljen s dva vertikalna pravca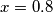 i
i 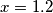 .
.
Kolika je vjerojatnost da se svih pet čestica nalaze između ova dva pravca nakon sekunde?
sekunde?
Pretpostavite da su čestice toliko malene da se ne mogu međusobno sudarati.
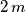 i visine
i visine 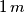 u donjem lijevom kutu spremnika(neka se donji lijevi kut nalazi u točki
u donjem lijevom kutu spremnika(neka se donji lijevi kut nalazi u točki 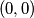 ) nalazi se
) nalazi se  jako malenih čestica od kojih svaka u trenutku
jako malenih čestica od kojih svaka u trenutku 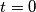 ima nasumičan vektor smjera određen preko nasumično odabrane točke iz ravnine i točke
ima nasumičan vektor smjera određen preko nasumično odabrane točke iz ravnine i točke 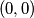 tako da je brzina iz
tako da je brzina iz ![[0,4] \, ms^{-1}](/media/m/c/5/b/c5b1d368916bceecdc716f53b6d9cf0b.png) i kut između
i kut između ![[0,\frac{\pi} {2}]](/media/m/c/4/4/c444f378dc333f50e2dba634ad695486.png) .
. Spremnik je podijeljen s dva vertikalna pravca
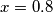 i
i 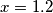 .
. Kolika je vjerojatnost da se svih pet čestica nalaze između ova dva pravca nakon
 sekunde?
sekunde? Pretpostavite da su čestice toliko malene da se ne mogu međusobno sudarati.
In the first quadrant of the coordinate system, there is a two-dimensional container of horizontal length 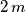 and height of
and height of 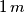 . In the left bottom part of the container (let that be point
. In the left bottom part of the container (let that be point 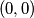 ) there are
) there are  extremely small particles, each of which in time
extremely small particles, each of which in time 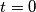 has a random direction vector determined with a random point from the plane and with point
has a random direction vector determined with a random point from the plane and with point 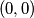 such that the velocity is between
such that the velocity is between ![[0,4] \, ms^{-1}](/media/m/c/5/b/c5b1d368916bceecdc716f53b6d9cf0b.png) and the angle is between
and the angle is between ![[0,\frac{\pi} {2}]]](/media/m/9/5/a/95aca457e2b03e659a0df09dd5784024.png) .
.
The container is divided into two parts by vertical lines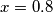 and
and 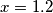 .
.
What's the probability that all five particles find themselves between those two lines after second?
second?
You may suppose that particles are so small that they cannot collide one with another.
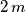 and height of
and height of 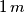 . In the left bottom part of the container (let that be point
. In the left bottom part of the container (let that be point 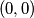 ) there are
) there are  extremely small particles, each of which in time
extremely small particles, each of which in time 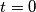 has a random direction vector determined with a random point from the plane and with point
has a random direction vector determined with a random point from the plane and with point 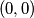 such that the velocity is between
such that the velocity is between ![[0,4] \, ms^{-1}](/media/m/c/5/b/c5b1d368916bceecdc716f53b6d9cf0b.png) and the angle is between
and the angle is between ![[0,\frac{\pi} {2}]]](/media/m/9/5/a/95aca457e2b03e659a0df09dd5784024.png) .
. The container is divided into two parts by vertical lines
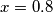 and
and 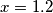 .
. What's the probability that all five particles find themselves between those two lines after
 second?
second? You may suppose that particles are so small that they cannot collide one with another.
