Vrijeme: 17:59
Dali smo mu ime! | We gave it a name! #4
Neka je 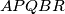 konveksan peterokut upisan u kružnicu čiji je promjer
konveksan peterokut upisan u kružnicu čiji je promjer  . Tangenta na kružnicu u
. Tangenta na kružnicu u  siječe pravce
siječe pravce 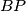 i
i 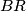 u
u  i
i  , redom. Pretpostavimo da
, redom. Pretpostavimo da 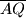 raspolavlja
raspolavlja 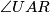 i da vrijedi
i da vrijedi 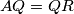 . Nađi minimalnu vrijednost izraza:
. Nađi minimalnu vrijednost izraza: 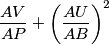 Odgovor zaokruži na
Odgovor zaokruži na  decimale.
decimale.
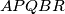 konveksan peterokut upisan u kružnicu čiji je promjer
konveksan peterokut upisan u kružnicu čiji je promjer  . Tangenta na kružnicu u
. Tangenta na kružnicu u  siječe pravce
siječe pravce 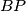 i
i 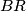 u
u  i
i  , redom. Pretpostavimo da
, redom. Pretpostavimo da 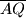 raspolavlja
raspolavlja 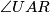 i da vrijedi
i da vrijedi 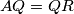 . Nađi minimalnu vrijednost izraza:
. Nađi minimalnu vrijednost izraza: 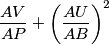 Odgovor zaokruži na
Odgovor zaokruži na  decimale.
decimale. Let 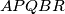 be a convex pentagon inscribed in a circle whose diameter is
be a convex pentagon inscribed in a circle whose diameter is  . The tangent to the circle in
. The tangent to the circle in  intersects the lines
intersects the lines 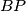 and
and 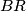 in
in  and
and  , respectively. Assume that
, respectively. Assume that 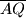 bisects
bisects 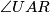 and
and 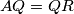 . Find the minimum value of the expression:
. Find the minimum value of the expression: 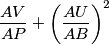 Round the answer to
Round the answer to  decimal places.
decimal places.
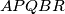 be a convex pentagon inscribed in a circle whose diameter is
be a convex pentagon inscribed in a circle whose diameter is  . The tangent to the circle in
. The tangent to the circle in  intersects the lines
intersects the lines 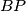 and
and 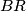 in
in  and
and  , respectively. Assume that
, respectively. Assume that 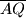 bisects
bisects 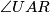 and
and 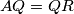 . Find the minimum value of the expression:
. Find the minimum value of the expression: 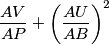 Round the answer to
Round the answer to  decimal places.
decimal places. 