Solve for

:
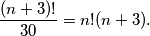 Note:
Note: For nonnegative integer

is
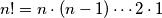
.
[lang=hr]
Odredite $n$ u jednadžbi $$\frac{(n+3)!}{30}=n!(n+3)\text{.}$$
\\
\textit{Napomena:} Za prirodan broj $n$ vrijedi $n!=n\cdot (n-1)\cdots 2 \cdot 1$.
[/lang]
[lang=en]
Solve for $n$: $$\frac{(n+3)!}{30}=n!(n+3)\text{.}$$
\\
\textit{Note:} For nonnegative integer $n$ is $n!=n\cdot (n-1)\cdots 2 \cdot 1$.
[/lang]