Vrijeme: 18:00
Koja jednadžba? | Equation, whaaat? #4
Dana je dužina 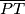 duljine
duljine  .
.  i
i  su na kružnicama
su na kružnicama  i
i  takvim da su im središta s različitih strana
takvim da su im središta s različitih strana 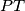 . Radius
. Radius  je
je 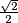 , a
, a  je
je 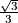 . Pravac kroz
. Pravac kroz  sijeće
sijeće  i
i  još u
još u  i
i  . Koliko je
. Koliko je 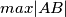 ?
?
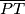 duljine
duljine  .
.  i
i  su na kružnicama
su na kružnicama  i
i  takvim da su im središta s različitih strana
takvim da su im središta s različitih strana 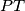 . Radius
. Radius  je
je 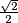 , a
, a  je
je 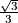 . Pravac kroz
. Pravac kroz  sijeće
sijeće  i
i  još u
još u  i
i  . Koliko je
. Koliko je 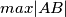 ?
? The length of 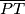 is
is  .
.  and
and  are on circles
are on circles  and
and  such that their centers are on different sides of
such that their centers are on different sides of 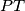 . The radius of
. The radius of  is
is 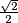 , and that of
, and that of  is
is 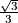 . The line passing through
. The line passing through  intersects
intersects  and
and  at
at  and
and  , respectively. What is the maximum value of
, respectively. What is the maximum value of 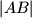 ?
?
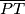 is
is  .
.  and
and  are on circles
are on circles  and
and  such that their centers are on different sides of
such that their centers are on different sides of 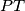 . The radius of
. The radius of  is
is 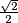 , and that of
, and that of  is
is 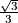 . The line passing through
. The line passing through  intersects
intersects  and
and  at
at  and
and  , respectively. What is the maximum value of
, respectively. What is the maximum value of 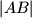 ?
? 