U trokutu
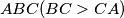
vrijedi
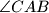
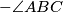
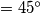
. Ako je

točka na stranici

takva da je
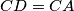
, izračunaj
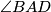
. Rješenje napiši u stupnjevima, zaokruženo na dvije decimale.
In the triangle
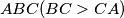
,
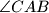
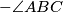
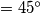
holds. If

is a point on the side

such that
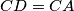
, calculate
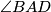
. Write the solution in degrees, rounded to two decimal places.
[lang = hr]
U trokutu $ABC (BC > CA)$ vrijedi $\angle CAB$ $- \angle ABC$ $ = 45^{\circ}$. Ako je $D$ točka na stranici $BC$ takva da je $CD = CA$, izračunaj $\angle BAD$. Rješenje napiši u stupnjevima, zaokruženo na dvije decimale.
[/lang]
[lang = en]
In the triangle $ABC (BC > CA)$, $\angle CAB$ $- \angle ABC$ $ = 45^{\circ}$ holds. If $D$ is a point on the side $BC$ such that $CD = CA$, calculate $\angle BAD$. Write the solution in degrees, rounded to two decimal places.
[/lang]