Vrijeme: 18:03
Povratak kutomjera | Return of the protractor #2
Neka su točke 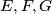 redom polovišta stranica
redom polovišta stranica 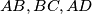 četverokuta
četverokuta  . Poznato je da je
. Poznato je da je 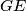 okomito na
okomito na  ,
, 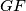 okomito na
okomito na  te da je
te da je 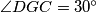 . Ako se pravci
. Ako se pravci  i
i  sijeku u
sijeku u  , pravci
, pravci  i
i  u
u  , a pravci
, a pravci  i
i  u
u  odredi
odredi 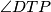 . Rješenje zaokruži na dvije decimale.
. Rješenje zaokruži na dvije decimale.
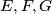 redom polovišta stranica
redom polovišta stranica 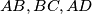 četverokuta
četverokuta  . Poznato je da je
. Poznato je da je 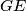 okomito na
okomito na  ,
, 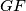 okomito na
okomito na  te da je
te da je 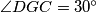 . Ako se pravci
. Ako se pravci  i
i  sijeku u
sijeku u  , pravci
, pravci  i
i  u
u  , a pravci
, a pravci  i
i  u
u  odredi
odredi 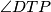 . Rješenje zaokruži na dvije decimale.
. Rješenje zaokruži na dvije decimale. Let the points 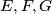 respectively be the halves of the sides
respectively be the halves of the sides 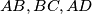 of the quadrilateral
of the quadrilateral  . It is known that
. It is known that 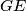 is perpendicular to
is perpendicular to  ,
, 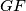 is perpendicular to
is perpendicular to  and that
and that 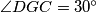 . If lines
. If lines  and
and  intersect in
intersect in  , lines
, lines  and
and  in
in  , and lines
, and lines  and
and  in
in  determine
determine 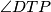 . Round the solution to two decimal places.
. Round the solution to two decimal places.
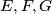 respectively be the halves of the sides
respectively be the halves of the sides 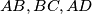 of the quadrilateral
of the quadrilateral  . It is known that
. It is known that 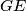 is perpendicular to
is perpendicular to  ,
, 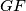 is perpendicular to
is perpendicular to  and that
and that 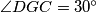 . If lines
. If lines  and
and  intersect in
intersect in  , lines
, lines  and
and  in
in  , and lines
, and lines  and
and  in
in  determine
determine 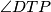 . Round the solution to two decimal places.
. Round the solution to two decimal places. 