Vrijeme: 18:00
Povratak kutomjera | Return of the protractor #3
U paralelogramu 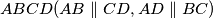 vrijedi
vrijedi  . Neka je
. Neka je  točka na dužini
točka na dužini  tako da vrijedi
tako da vrijedi 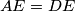 . Pravac
. Pravac  siječe dužinu
siječe dužinu  u točki
u točki  . Ispostavilo se da je pravac
. Ispostavilo se da je pravac 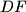 simetrala
simetrala 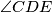 . Izračunaj
. Izračunaj 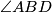 . Rješenje zaokruži na dvije decimale.
. Rješenje zaokruži na dvije decimale.
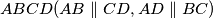 vrijedi
vrijedi  . Neka je
. Neka je  točka na dužini
točka na dužini  tako da vrijedi
tako da vrijedi 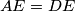 . Pravac
. Pravac  siječe dužinu
siječe dužinu  u točki
u točki  . Ispostavilo se da je pravac
. Ispostavilo se da je pravac 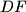 simetrala
simetrala 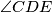 . Izračunaj
. Izračunaj 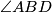 . Rješenje zaokruži na dvije decimale.
. Rješenje zaokruži na dvije decimale. In the parallelogram 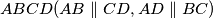
 holds. Let
holds. Let  be a point on the length
be a point on the length  such that
such that 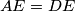 holds. Line
holds. Line  intersects length
intersects length  at point
at point  . It turns out that the line
. It turns out that the line 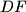 is the bisector of
is the bisector of 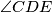 . Calculate
. Calculate 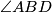 . Round the solution to two decimal places.
. Round the solution to two decimal places.
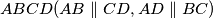
 holds. Let
holds. Let  be a point on the length
be a point on the length  such that
such that 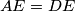 holds. Line
holds. Line  intersects length
intersects length  at point
at point  . It turns out that the line
. It turns out that the line 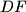 is the bisector of
is the bisector of 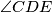 . Calculate
. Calculate 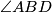 . Round the solution to two decimal places.
. Round the solution to two decimal places. 