Vrijeme: 18:00
Povratak kutomjera | Return of the protractor #5
Neka je  trokut u kome je
trokut u kome je 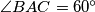 . Neka su
. Neka su 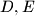 točke na
točke na  i
i  redom takve da je
redom takve da je  simetrala
simetrala  i
i  je simetrala
je simetrala  . Ako vrijedi
. Ako vrijedi 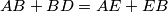 , koliko je
, koliko je 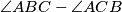 ? Rješenje zaokruži na dvije decimale.
? Rješenje zaokruži na dvije decimale.
 trokut u kome je
trokut u kome je 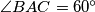 . Neka su
. Neka su 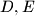 točke na
točke na  i
i  redom takve da je
redom takve da je  simetrala
simetrala  i
i  je simetrala
je simetrala  . Ako vrijedi
. Ako vrijedi 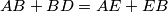 , koliko je
, koliko je 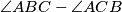 ? Rješenje zaokruži na dvije decimale.
? Rješenje zaokruži na dvije decimale. Let  be a triangle in which
be a triangle in which 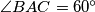 . Let
. Let 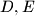 be points on
be points on  and
and  respectively such that
respectively such that  is the bisector of
is the bisector of  and
and  is the bisector of
is the bisector of  . If
. If 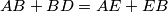 holds, what is
holds, what is 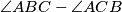 ? Round the solution to two decimal places.
? Round the solution to two decimal places.
 be a triangle in which
be a triangle in which 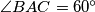 . Let
. Let 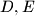 be points on
be points on  and
and  respectively such that
respectively such that  is the bisector of
is the bisector of  and
and  is the bisector of
is the bisector of  . If
. If 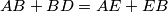 holds, what is
holds, what is 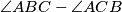 ? Round the solution to two decimal places.
? Round the solution to two decimal places. 