Neka je

konveksan četverokut čiji je opseg

u kome vrijedi
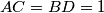
. Koliko najvište može iznositi površina četverokuta

? Odgovor zaokruži na

decimala.
Let

be a convex quadrilateral whose perimeter is

in which
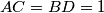
holds. What is the maximum area of quadrilateral

? Round the answer to 5 decimal places.
[lang = hr]
Neka je $ABCD$ konveksan četverokut čiji je opseg $\tfrac{5}{2}$ u kome vrijedi $AC=BD=1$. Koliko najvište može iznositi površina četverokuta $ABCD$? Odgovor zaokruži na $5$ decimala.
[/lang]
[lang = en]
Let $ABCD$ be a convex quadrilateral whose perimeter is $\tfrac{5}{2}$ in which $AC=BD=1$ holds. What is the maximum area of quadrilateral $ABCD$? Round the answer to 5 decimal places.
[/lang]