Vrijeme: 04:17
Veoma nasumičan geometrijski lanac | Pretty random geometry chain #3
Niki and Kyle play a triangle game. Niki first draws  with area
with area  , and Kyle picks a point
, and Kyle picks a point  inside
inside  . Niki then draws segments
. Niki then draws segments 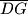 ,
, 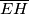 , and
, and 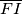 , all through
, all through  , such that
, such that  and
and  are on
are on 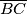 ,
,  and
and  are on
are on 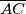 , and
, and  and
and  are on
are on 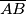 . The ten points must all be distinct. Finally, let
. The ten points must all be distinct. Finally, let  be the sum of the areas of triangles
be the sum of the areas of triangles 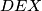 ,
, 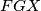 , and
, and 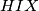 . Kyle earns
. Kyle earns  points, and Niki earns
points, and Niki earns 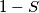 points. If both players play optimally to maximize the amount of points they get, who will win and by how much? Write your answer in the form "XY" where X is the first letter of the winner's name and Y is a difference rounded to
points. If both players play optimally to maximize the amount of points they get, who will win and by how much? Write your answer in the form "XY" where X is the first letter of the winner's name and Y is a difference rounded to  decimal places.
decimal places.
 with area
with area  , and Kyle picks a point
, and Kyle picks a point  inside
inside  . Niki then draws segments
. Niki then draws segments 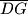 ,
, 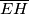 , and
, and 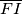 , all through
, all through  , such that
, such that  and
and  are on
are on 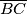 ,
,  and
and  are on
are on 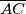 , and
, and  and
and  are on
are on 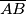 . The ten points must all be distinct. Finally, let
. The ten points must all be distinct. Finally, let  be the sum of the areas of triangles
be the sum of the areas of triangles 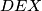 ,
, 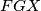 , and
, and 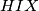 . Kyle earns
. Kyle earns  points, and Niki earns
points, and Niki earns 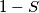 points. If both players play optimally to maximize the amount of points they get, who will win and by how much? Write your answer in the form "XY" where X is the first letter of the winner's name and Y is a difference rounded to
points. If both players play optimally to maximize the amount of points they get, who will win and by how much? Write your answer in the form "XY" where X is the first letter of the winner's name and Y is a difference rounded to  decimal places.
decimal places. Niki and Kyle play a triangle game. Niki first draws  with area
with area  , and Kyle picks a point
, and Kyle picks a point  inside
inside  . Niki then draws segments
. Niki then draws segments 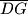 ,
, 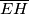 , and
, and 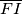 , all through
, all through  , such that
, such that  and
and  are on
are on 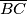 ,
,  and
and  are on
are on 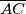 , and
, and  and
and  are on
are on 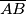 . The ten points must all be distinct. Finally, let
. The ten points must all be distinct. Finally, let  be the sum of the areas of triangles
be the sum of the areas of triangles 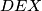 ,
, 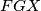 , and
, and 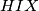 . Kyle earns
. Kyle earns  points, and Niki earns
points, and Niki earns 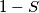 points. If both players play optimally to maximize the amount of points they get, who will win and by how much? Write your answer in the form "XY" where X is the first letter of the winner's name and Y is a difference rounded to
points. If both players play optimally to maximize the amount of points they get, who will win and by how much? Write your answer in the form "XY" where X is the first letter of the winner's name and Y is a difference rounded to  decimal places.
decimal places.
 with area
with area  , and Kyle picks a point
, and Kyle picks a point  inside
inside  . Niki then draws segments
. Niki then draws segments 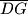 ,
, 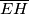 , and
, and 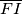 , all through
, all through  , such that
, such that  and
and  are on
are on 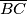 ,
,  and
and  are on
are on 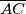 , and
, and  and
and  are on
are on 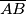 . The ten points must all be distinct. Finally, let
. The ten points must all be distinct. Finally, let  be the sum of the areas of triangles
be the sum of the areas of triangles 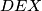 ,
, 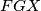 , and
, and 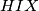 . Kyle earns
. Kyle earns  points, and Niki earns
points, and Niki earns 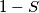 points. If both players play optimally to maximize the amount of points they get, who will win and by how much? Write your answer in the form "XY" where X is the first letter of the winner's name and Y is a difference rounded to
points. If both players play optimally to maximize the amount of points they get, who will win and by how much? Write your answer in the form "XY" where X is the first letter of the winner's name and Y is a difference rounded to  decimal places.
decimal places. 