Vrijeme: 17:58
Veoma nasumičan geometrijski lanac | Pretty random geometry chain #4
U unutrašnjosti trokuta  u kome je
u kome je 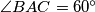 i
i 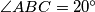 uočena je točka
uočena je točka  takva da je
takva da je 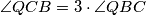 . Simetrale
. Simetrale 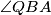 i
i 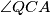 sijeku se u točki P, pri čemu je
sijeku se u točki P, pri čemu je 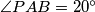 . Nađi
. Nađi 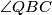 . Rješenje zaokruži na dvije decimale.
. Rješenje zaokruži na dvije decimale.
 u kome je
u kome je 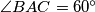 i
i 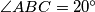 uočena je točka
uočena je točka  takva da je
takva da je 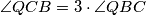 . Simetrale
. Simetrale 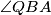 i
i 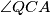 sijeku se u točki P, pri čemu je
sijeku se u točki P, pri čemu je 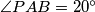 . Nađi
. Nađi 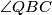 . Rješenje zaokruži na dvije decimale.
. Rješenje zaokruži na dvije decimale. In the interior of the triangle  in which
in which 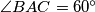 and
and 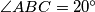 the point
the point  was observed such that
was observed such that 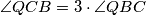 . Bisectors
. Bisectors 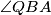 and
and 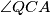 intersect at point P, where
intersect at point P, where 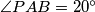 . Find
. Find 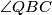 . Round the solution to two decimal places.
. Round the solution to two decimal places.
 in which
in which 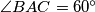 and
and 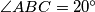 the point
the point  was observed such that
was observed such that 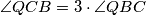 . Bisectors
. Bisectors 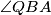 and
and 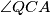 intersect at point P, where
intersect at point P, where 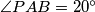 . Find
. Find 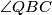 . Round the solution to two decimal places.
. Round the solution to two decimal places. 