Vrijeme: 04:16
Veoma nasumičan geometrijski lanac | Pretty random geometry chain #5
Let  be a circle with center
be a circle with center  and radius
and radius  , and let
, and let  be a point such that
be a point such that 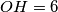 . A point
. A point  is called special if, for all triangles
is called special if, for all triangles  with circumcircle
with circumcircle  and orthocenter
and orthocenter  , we have that
, we have that  lies on
lies on 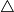 ABC or in the interior of
ABC or in the interior of 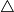 ABC. Find the area of the region consisting of all special points.Round your solution to
ABC. Find the area of the region consisting of all special points.Round your solution to  decimal places.
decimal places.
 be a circle with center
be a circle with center  and radius
and radius  , and let
, and let  be a point such that
be a point such that 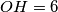 . A point
. A point  is called special if, for all triangles
is called special if, for all triangles  with circumcircle
with circumcircle  and orthocenter
and orthocenter  , we have that
, we have that  lies on
lies on 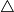 ABC or in the interior of
ABC or in the interior of 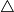 ABC. Find the area of the region consisting of all special points.Round your solution to
ABC. Find the area of the region consisting of all special points.Round your solution to  decimal places.
decimal places. Let  be a circle with center
be a circle with center  and radius
and radius  , and let
, and let  be a point such that
be a point such that 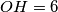 . A point
. A point  is called special if, for all triangles
is called special if, for all triangles  with circumcircle
with circumcircle  and orthocenter
and orthocenter  , we have that
, we have that  lies on
lies on 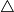 ABC or in the interior of
ABC or in the interior of  ABC. Find the area of the region consisting of all special points. Round your solution to
ABC. Find the area of the region consisting of all special points. Round your solution to  decimal places.
decimal places.
 be a circle with center
be a circle with center  and radius
and radius  , and let
, and let  be a point such that
be a point such that 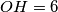 . A point
. A point  is called special if, for all triangles
is called special if, for all triangles  with circumcircle
with circumcircle  and orthocenter
and orthocenter  , we have that
, we have that  lies on
lies on  ABC or in the interior of
ABC or in the interior of  ABC. Find the area of the region consisting of all special points. Round your solution to
ABC. Find the area of the region consisting of all special points. Round your solution to  decimal places.
decimal places. 