Vrijeme: 18:03
Raspiši mi duljinu | Length bashing #2
Na stranici  trokuta
trokuta  izabrana je točka
izabrana je točka  takva da vrijedi
takva da vrijedi 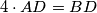 . Točke
. Točke 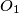 i
i 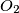 su središta kružnica opisanih oko trokuta
su središta kružnica opisanih oko trokuta  i
i 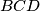 . Pretpostavimo da je
. Pretpostavimo da je 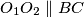 . Pravac
. Pravac 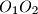 dijeli trokut
dijeli trokut  na dva dijela površina
na dva dijela površina 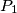 i
i 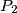 . Ako je
. Ako je 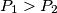 odredi
odredi 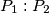 . Odgovor zaokruži na
. Odgovor zaokruži na  decimale.
decimale.
 trokuta
trokuta  izabrana je točka
izabrana je točka  takva da vrijedi
takva da vrijedi 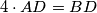 . Točke
. Točke 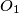 i
i 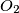 su središta kružnica opisanih oko trokuta
su središta kružnica opisanih oko trokuta  i
i 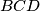 . Pretpostavimo da je
. Pretpostavimo da je 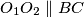 . Pravac
. Pravac 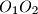 dijeli trokut
dijeli trokut  na dva dijela površina
na dva dijela površina 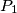 i
i 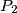 . Ako je
. Ako je 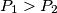 odredi
odredi 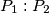 . Odgovor zaokruži na
. Odgovor zaokruži na  decimale.
decimale. On side  of the triangle
of the triangle  choose point
choose point  such that
such that 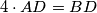 . Points
. Points 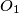 and
and 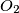 are centers of circumscribed circles of triangles
are centers of circumscribed circles of triangles  and
and 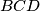 respectively. Suppose
respectively. Suppose 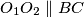 . Line
. Line 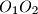 divides triangle
divides triangle  in two parts with areas
in two parts with areas 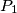 and
and 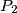 . Suppose
. Suppose 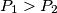 . Find
. Find 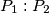 . Round your answer to three decimal places.
. Round your answer to three decimal places.
 of the triangle
of the triangle  choose point
choose point  such that
such that 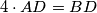 . Points
. Points 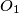 and
and 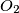 are centers of circumscribed circles of triangles
are centers of circumscribed circles of triangles  and
and 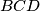 respectively. Suppose
respectively. Suppose 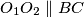 . Line
. Line 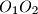 divides triangle
divides triangle  in two parts with areas
in two parts with areas 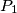 and
and 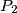 . Suppose
. Suppose 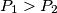 . Find
. Find 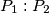 . Round your answer to three decimal places.
. Round your answer to three decimal places. 