Vrijeme: 18:02
Raspiši mi duljinu | Length bashing #5
U trokutu  ,
, 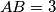 ,
, 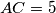 i
i 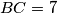 . Neka je
. Neka je  osnosimetrična točka točki
osnosimetrična točka točki  s obzirom na pravac
s obzirom na pravac  i neka je pravac
i neka je pravac  siječe trokutu
siječe trokutu  opisanu kružnicu u točki
opisanu kružnicu u točki  ,
, 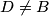 . Neka je
. Neka je  središte trokutu
središte trokutu  upisane kružnice. Odredi
upisane kružnice. Odredi 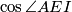 . Odgovor zaokružite na tri decimale.
. Odgovor zaokružite na tri decimale.
 ,
, 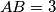 ,
, 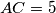 i
i 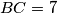 . Neka je
. Neka je  osnosimetrična točka točki
osnosimetrična točka točki  s obzirom na pravac
s obzirom na pravac  i neka je pravac
i neka je pravac  siječe trokutu
siječe trokutu  opisanu kružnicu u točki
opisanu kružnicu u točki  ,
, 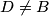 . Neka je
. Neka je  središte trokutu
središte trokutu  upisane kružnice. Odredi
upisane kružnice. Odredi 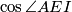 . Odgovor zaokružite na tri decimale.
. Odgovor zaokružite na tri decimale. In triangle  ,
, 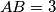 ,
, 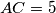 , and
, and 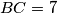 . Let
. Let  be the reflection of
be the reflection of  over line
over line  , and let line
, and let line  meet the circumcircle of
meet the circumcircle of  again at
again at  . Let
. Let  be the incenter of
be the incenter of 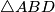 . Find
. Find 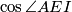 . Round your answer to
. Round your answer to  decimal places.
decimal places.
 ,
, 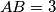 ,
, 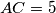 , and
, and 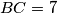 . Let
. Let  be the reflection of
be the reflection of  over line
over line  , and let line
, and let line  meet the circumcircle of
meet the circumcircle of  again at
again at  . Let
. Let  be the incenter of
be the incenter of 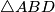 . Find
. Find 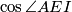 . Round your answer to
. Round your answer to  decimal places.
decimal places. 