Vrijeme: 18:31
Ukrainski lanac | Ukraine chain #2
Taras ima prijatelja, Mykolu. S vremena na vrijeme igraju igru: Mykola crta ploču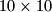 
i također crta plus ili minus u svakoj od njenih ćelija (različite ćelije mogu imati različite simbole). Tada dolazi Taras: u jednom potezu Taras može odabrati bilo koji cross, tj. uniju retka i stupca, i promijeniti znakove u njemu suprotnim. Za svaki potez Taras mora platiti jednu grivnu. Koliki je najmanji iznos grivni koji Taras mora imati kako bi bez obzira na početnu ploču uvijek mogao promijeniti ploču na sve pluseve?
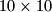i također crta plus ili minus u svakoj od njenih ćelija (različite ćelije mogu imati različite simbole). Tada dolazi Taras: u jednom potezu Taras može odabrati bilo koji cross, tj. uniju retka i stupca, i promijeniti znakove u njemu suprotnim. Za svaki potez Taras mora platiti jednu grivnu. Koliki je najmanji iznos grivni koji Taras mora imati kako bi bez obzira na početnu ploču uvijek mogao promijeniti ploču na sve pluseve? Taras has a buddy, Mykola. Every once in a while they play a game: Mykola draws a board 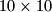and also draws a plus or a minus in each of its cells (different cells might have different symbols). Then Taras comes in: in one move Taras can select any cross, i.e. union of a row and a column, and change the signs in it to the opposite ones. For each move Taras has to pay one hryvnia. What is the smallest amount of hryvnias does Taras have to have so that no matter what the initial board is he can always change it to all-pluses-board?
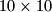and also draws a plus or a minus in each of its cells (different cells might have different symbols). Then Taras comes in: in one move Taras can select any cross, i.e. union of a row and a column, and change the signs in it to the opposite ones. For each move Taras has to pay one hryvnia. What is the smallest amount of hryvnias does Taras have to have so that no matter what the initial board is he can always change it to all-pluses-board?