Marinada '23

[lang = hr] Taras voli šah. Naravno da voli. Štoviše, budući da sebe doživljava kao kralja programiranja, najviše voli kraljeve iz igre. On čak smatra da je \textit{distance} između dvije ćelije na ploči minimalna količina koraka koju kralj treba da prijeđe od jedne do druge. Jednog dana Taras je imao previše toga na pretek, pa je obojio nekoliko polja na ploči 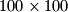$100 \times 100$ na način da ne postoje dvije ćelije tako da je udaljenost (koju je on definirao) između njih točno $15$. Koju je najveću količinu stanica mogao obojiti? [/lang] [lang = en] Taras loves chess. Of course he does. Moreover, since he views himself as a king of programming, he likes the kings from the game the most. He even thinks of a \textit{distance} between two cells on a board as the minimal amount of steps a king needs to get from one of them to another. One day Taras got way too much to spare, so he coloured several squares on the board 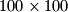$100 \times 100$ in a way that there are no two cells such that the distance (that he defined) between them is exactly $15$. What is the biggest amount of cells could he colour? [/lang]