Vrijeme: 11:13
Ukrainski lanac | Ukraine chain #6
Jedna od drugih stvari koje Taras voli crtati su takozvani plus-shapes: unija pravokutnika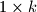 
s pravokutnikom 
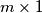(za neke 
i 
) koji se sijeku na jednom kvadratu koji nije krajnji lijevi/krajnji desni ili krajnji gornji/donji kvadrat za bilo koji od pravokutnika (tj. tako da dobiveni oblik nalikuje plusu, a ne slovu "T" ili "L" ili nečem drugom) . Plus-oblik ne mora biti simetričan. Na koliko načina može obojiti u žuto neka od polja na ploči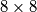 
, tako da žuta polja formiraju plus?
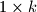s pravokutnikom 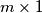(za neke i ) koji se sijeku na jednom kvadratu koji nije krajnji lijevi/krajnji desni ili krajnji gornji/donji kvadrat za bilo koji od pravokutnika (tj. tako da dobiveni oblik nalikuje plusu, a ne slovu "T" ili "L" ili nečem drugom) . Plus-oblik ne mora biti simetričan. Na koliko načina može obojiti u žuto neka od polja na ploči 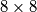, tako da žuta polja formiraju plus?Veliko hvala Arseniju Nikolaevu, osnivaču Quanta, koji je poslao ovaj lanac!
One of the other things Taras likes to draw are the so-called plus-shapes: a union of a rectangle 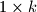with a rectangle 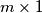(for some and ) that intersect at one square which is not the leftmost/rightmost or uppermost/bottom square for any of the rectangles (i.e so that the resulting shape resembles a plus, and not a letter "T" or "L" or something else). A plus-shape does not have to be symmetric. In how many ways, can he colour yellow some of the squares on the board 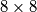, so that the yellow squares form a plus-shape?
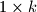with a rectangle 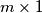(for some and ) that intersect at one square which is not the leftmost/rightmost or uppermost/bottom square for any of the rectangles (i.e so that the resulting shape resembles a plus, and not a letter "T" or "L" or something else). A plus-shape does not have to be symmetric. In how many ways, can he colour yellow some of the squares on the board 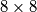, so that the yellow squares form a plus-shape?Big thanks to Arsenii Nikolaev, founder of Quanta, who send this chain!