Let
be real sequence defined by
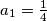
and the recurrence
.
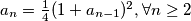
Find the minimum real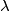 
such that for any non-negative reals 
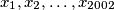, it holds 
where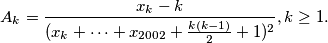 
Neka je
realni niz definiran s
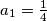
i s rekurzijom
.
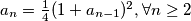
Odredite minimum realnog broja
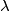
tako da za svaki nenegativni realni broj
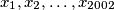
vrijedi
gdje
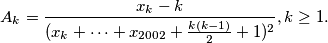
[lang=en]
Let $(a_n)_{n\in \mathbb{N}}$ be real sequence defined by $ a_{1}=\frac{1}{4}$ and the recurrence $ a_{n}= \frac{1}{4}(1+a_{n-1})^{2}, \forall n\geq 2$.
Find the minimum real $ \lambda$ such that for any non-negative reals $ x_{1},x_{2},\dots,x_{2002}$, it holds \[ \sum_{k=1}^{2002}A_{k}\leq \lambda a_{2002}, \] where \[ A_{k}= \frac{x_{k}-k}{(x_{k}+\cdots+x_{2002}+\frac{k(k-1)}{2}+1)^{2}}, k \geq 1.\]
[/lang]
[lang=hr]
Neka je $(a_n)_{n\in \mathbb{N}}$ realni niz definiran s $ a_{1}=\frac{1}{4}$ i s rekurzijom $ a_{n}= \frac{1}{4}(1+a_{n-1})^{2}, \forall n\geq 2$.
\\
Odredite minimum realnog broja $ \lambda$ tako da za svaki nenegativni realni broj $ x_{1},x_{2},\dots,x_{2002}$ vrijedi \[ \sum_{k=1}^{2002}A_{k}\leq \lambda a_{2002}, \]
gdje
\[ A_{k}= \frac{x_{k}-k}{(x_{k}+\cdots+x_{2002}+\frac{k(k-1)}{2}+1)^{2}}, k \geq 1.\]
[/lang]
