Neka je

niz realnih brojeva s
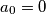
,
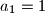
i takav da za svaki prirodan broj
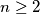
postoji prirodan broj
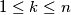
za koji vrijedi
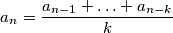
Odredite najveću vrijednost izraza

.
Let

be a series of real numbers where
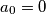
,
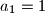
and where for every natural number
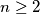
exists a natural number
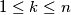
for which
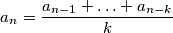
Determine the maximum value of

.
[lang=hr]
Neka je $a_n$ niz realnih brojeva s $a_0=0$, $a_1=1$ i takav da za svaki prirodan broj $n\geq2$ postoji prirodan broj $1\leq k\leq n$ za koji vrijedi $$a_n=\frac{a_{n-1}+\ldots+a_{n-k}}{k}$$ Odredite najveću vrijednost izraza $a_{2024}-a_{2023}$.
[/lang]
[lang=en]
Let $a_n$ be a series of real numbers where $a_0=0$, $a_1=1$ and where for every natural number $n\geq2$ exists a natural number $1\leq k\leq n$ for which
$$a_n=\frac{a_{n-1}+\ldots+a_{n-k}}{k}$$
Determine the maximum value of $a_{2024}-a_{2023}$.
[/lang]