Let

be a real function with real variables such that:
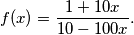
Determine
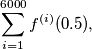
where
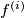
is the

-th composition of the function.
[lang=hr]
Neka je zadana realna funkcija realne varijable s pravilom pridruživanja$$f(x)=\frac{1+10x}{10-100x}.$$
Odredi $$\sum_{i=1}^{6000}f^{(i)}(0.5),$$
\\
gdje $f^{(i)}$ označava $i$-tu kompoziciju.
[/lang]
[lang=en]
Let $f(x)$ be a real function with real variables such that:
$$f(x)=\frac{1+10x}{10-100x}.$$
Determine
$$\sum_{i=1}^{6000}f^{(i)}(0.5),$$
where $f^{(i)}$ is the $i$-th composition of the function.
[/lang]