Vrijeme: 05:31
Based vjerojatnost | Based probability #4
Pošto Mateju sama informacija o idealnom  nije jako korisna, pogotovo jer je vjerojatnost bilo kojeg specifičnog
nije jako korisna, pogotovo jer je vjerojatnost bilo kojeg specifičnog  nula (jer postoji neprebrojivo mnogo mogućih odabira za
nula (jer postoji neprebrojivo mnogo mogućih odabira za  ), odlučio se zapitati koja je vjerojatnost da je
), odlučio se zapitati koja je vjerojatnost da je  u intervalu
u intervalu ![[0.6, 0.7]](/media/m/1/7/1/1716fd1d66ab8346848e26197ed4705f.png) .
.
 nije jako korisna, pogotovo jer je vjerojatnost bilo kojeg specifičnog
nije jako korisna, pogotovo jer je vjerojatnost bilo kojeg specifičnog  nula (jer postoji neprebrojivo mnogo mogućih odabira za
nula (jer postoji neprebrojivo mnogo mogućih odabira za  ), odlučio se zapitati koja je vjerojatnost da je
), odlučio se zapitati koja je vjerojatnost da je  u intervalu
u intervalu ![[0.6, 0.7]](/media/m/1/7/1/1716fd1d66ab8346848e26197ed4705f.png) .
.Podsjećamo vas da je Mateju taj  bio nepoznat prije bacanja pa pretpostavlja da je vjerojatnost da je izabran bilo koji
bio nepoznat prije bacanja pa pretpostavlja da je vjerojatnost da je izabran bilo koji  iz intervala
iz intervala ![[0, 1]](/media/m/7/f/0/7f04c41d91b0555ac792351e836cbd4e.png) jednaka. Zatim su se desila tri bacanja, te su završila s dva pisma i jednom glavom.
jednaka. Zatim su se desila tri bacanja, te su završila s dva pisma i jednom glavom.
Odredi, iz Matejeve perspektive, koja je vjerojatnost da je 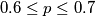 .
.
Since the information about the ideal  is not very useful to Matej, especially because the probability of any specific
is not very useful to Matej, especially because the probability of any specific  is zero (as there are uncountably many possible choices for
is zero (as there are uncountably many possible choices for  ), he decided to ask what the probability is that
), he decided to ask what the probability is that  lies in the interval
lies in the interval ![[0.6, 0.7]](/media/m/1/7/1/1716fd1d66ab8346848e26197ed4705f.png) .
.
 is not very useful to Matej, especially because the probability of any specific
is not very useful to Matej, especially because the probability of any specific  is zero (as there are uncountably many possible choices for
is zero (as there are uncountably many possible choices for  ), he decided to ask what the probability is that
), he decided to ask what the probability is that  lies in the interval
lies in the interval ![[0.6, 0.7]](/media/m/1/7/1/1716fd1d66ab8346848e26197ed4705f.png) .
.We remind you that before the coin tosses, Matej did not know  , so he assumes that the probability of choosing any
, so he assumes that the probability of choosing any  from the interval
from the interval ![[0, 1]](/media/m/7/f/0/7f04c41d91b0555ac792351e836cbd4e.png) is uniform. Then, three coin tosses occurred, resulting in two tails and one head.
is uniform. Then, three coin tosses occurred, resulting in two tails and one head.
Determine, from Matej's perspective, the probability that 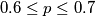 .
.
