Neka je

najveća konstanta takva da za sve realne
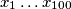
vrijedi:
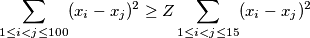
Odredite cijeli broj najbliži broju 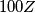 .
.
Let

be the largest constant such that for all real numbers
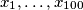
, the following inequality holds:
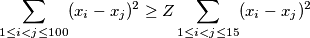
Determine the integer closest to 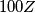 .
.
[lang=hr]
Neka je $Z$ najveća konstanta takva da za sve realne $x_1 \dots x_{100}$ vrijedi:
\[\sum_{1 \le i < j \le 100}(x_i-x_j)^2 \ge Z \sum_{1 \le i < j \le 15} (x_i-x_j)^2\]
Odredite cijeli broj najbliži broju $100Z$.
[/lang]
[lang=en]
Let $Z$ be the largest constant such that for all real numbers $x_1, \dots, x_{100}$, the following inequality holds:
\[\sum_{1 \le i < j \le 100}(x_i-x_j)^2 \ge Z \sum_{1 \le i < j \le 15} (x_i-x_j)^2\]
Determine the integer closest to $100Z$.
[/lang]