Odredite najveću konstantu

takvu da, za sve prirodne

i realne
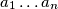
vrijedi:
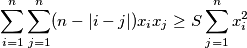 .
.
Determine the largest constant

such that for all natural numbers

and real numbers
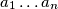
, the following inequality holds:
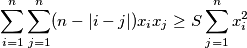 .
.
[lang=hr]
Odredite najveću konstantu $S$ takvu da, za sve prirodne $n$ i realne $a_1 \dots a_n$ vrijedi:
$$\sum_{i=1}^{n}\sum_{j=1}^{n}(n-|i-j|)x_ix_j \geq S\sum_{j=1}^{n}x^2_i$$.
[/lang]
[lang=en]
Determine the largest constant $S$ such that for all natural numbers $n$ and real numbers $a_1 \dots a_n$, the following inequality holds:
$$\sum_{i=1}^{n}\sum_{j=1}^{n}(n-|i-j|)x_ix_j \geq S\sum_{j=1}^{n}x^2_i$$.
[/lang]