Za prirodan broj
neka je
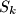
skup svih uređenih trojki
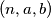
takve da je:
neparan,
,
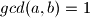
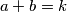
i
.
Nađi najveći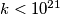 
takav da je 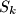konačan.
For a natural number
, let
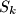
be the set of all ordered triples
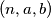
such that:
is odd,
,
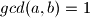
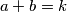
, and
.
Find the largest 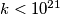such that 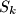is finite.
[lang=hr]
Za prirodan broj $k>1$ neka je $S_k$ skup svih uređenih trojki $(n,a,b)$ takve da je: $n$ neparan, $gcd(a,b)=1$, $a+b=k$ i $n | a^n+b^n$.
Nađi najveći $k<10^{21}$ takav da je $S_k$ konačan.
[/lang]
[lang=en]
For a natural number $k>1$, let $S_k$ be the set of all ordered triples $(n,a,b)$ such that: $n$ is odd, $gcd(a,b)=1$, $a+b=k$, and $n | a^n+b^n$.
Find the largest $k<10^{21}$ such that $S_k$ is finite.
[/lang]
