Vrijeme: 05:30
Nizovi | Sequences #4
Za svaki pozitivni realni broj 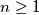 definiramo rekurzivnu relaciju sa
definiramo rekurzivnu relaciju sa  . Ako vrijedi
. Ako vrijedi 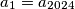 , pronađite zbroj kvadrata svih mogućih vrijednosti
, pronađite zbroj kvadrata svih mogućih vrijednosti  . Rješenje napišite kao decimalni broj zaokružen na dvije decimale. Koristite decimalnu točku (npr. 2.10).
. Rješenje napišite kao decimalni broj zaokružen na dvije decimale. Koristite decimalnu točku (npr. 2.10).
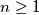 definiramo rekurzivnu relaciju sa
definiramo rekurzivnu relaciju sa  . Ako vrijedi
. Ako vrijedi 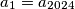 , pronađite zbroj kvadrata svih mogućih vrijednosti
, pronađite zbroj kvadrata svih mogućih vrijednosti  . Rješenje napišite kao decimalni broj zaokružen na dvije decimale. Koristite decimalnu točku (npr. 2.10).
. Rješenje napišite kao decimalni broj zaokružen na dvije decimale. Koristite decimalnu točku (npr. 2.10). For each positive integer 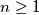 , we define the recursive relation given by
, we define the recursive relation given by  . Suppose that
. Suppose that 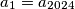 . Find the sum of the squares of all possible values of
. Find the sum of the squares of all possible values of  . Enter the solution as a decimal number rounded to two decimal places. Use a decimal point (e.g. 2.10).
. Enter the solution as a decimal number rounded to two decimal places. Use a decimal point (e.g. 2.10).
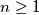 , we define the recursive relation given by
, we define the recursive relation given by  . Suppose that
. Suppose that 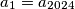 . Find the sum of the squares of all possible values of
. Find the sum of the squares of all possible values of  . Enter the solution as a decimal number rounded to two decimal places. Use a decimal point (e.g. 2.10).
. Enter the solution as a decimal number rounded to two decimal places. Use a decimal point (e.g. 2.10). 