Vrijeme: 06:58
Sigma lanac | Sigma chain #1
Suma
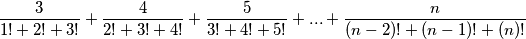
može se zapisati kao 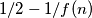 , gdje je
, gdje je  funkcija u
funkcija u  . Pokazuje se da je
. Pokazuje se da je  cjelobrojan, a mi vas pitamo da napišete najmanji
cjelobrojan, a mi vas pitamo da napišete najmanji  takav da je
takav da je  djeljiv s
djeljiv s 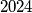 . Ako takav ne postoji, vratite
. Ako takav ne postoji, vratite  .
.
The sum
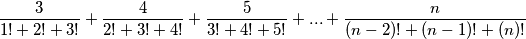
can be written as 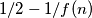 , where
, where  is a function of
is a function of  . It has been shown that
. It has been shown that  is an integer, and we ask you to find the smallest
is an integer, and we ask you to find the smallest  such that
such that  is divisible by
is divisible by 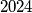 . If no such
. If no such  exists, return
exists, return  .
.
