Vrijeme: 05:31
Sigma lanac | Sigma chain #3
Suma 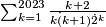 je udaljena za
je udaljena za  od najbližeg cijelog broja. Neka je
od najbližeg cijelog broja. Neka je 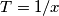 , ispostavi se da je to velik velik prirodan broj, a ako ga ne želite vratiti cijelog bit ćemo zadovoljni i sa ostatkom koji daje pri dijeljenju s
, ispostavi se da je to velik velik prirodan broj, a ako ga ne želite vratiti cijelog bit ćemo zadovoljni i sa ostatkom koji daje pri dijeljenju s 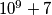 .
.
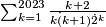 je udaljena za
je udaljena za  od najbližeg cijelog broja. Neka je
od najbližeg cijelog broja. Neka je 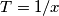 , ispostavi se da je to velik velik prirodan broj, a ako ga ne želite vratiti cijelog bit ćemo zadovoljni i sa ostatkom koji daje pri dijeljenju s
, ispostavi se da je to velik velik prirodan broj, a ako ga ne želite vratiti cijelog bit ćemo zadovoljni i sa ostatkom koji daje pri dijeljenju s 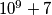 .
. The sum 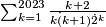 is a distance of
is a distance of  from the nearest integer. Let
from the nearest integer. Let 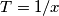 . It turns out that
. It turns out that  is a very large natural number, but if you don't want to find the whole number, we will be satisfied with the remainder when
is a very large natural number, but if you don't want to find the whole number, we will be satisfied with the remainder when  is divided by
is divided by 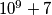 .
.
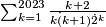 is a distance of
is a distance of  from the nearest integer. Let
from the nearest integer. Let 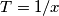 . It turns out that
. It turns out that  is a very large natural number, but if you don't want to find the whole number, we will be satisfied with the remainder when
is a very large natural number, but if you don't want to find the whole number, we will be satisfied with the remainder when  is divided by
is divided by 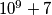 .
. 