Vrijeme: 05:32
Konstruktivne kritike | Constructive criticism #2
Dana je kružnica  radijusa
radijusa  sa središtem u
sa središtem u  te točka
te točka  na kružnici. Neka je
na kružnici. Neka je  polovište dužine
polovište dužine  i neka okomica na
i neka okomica na  u
u  siječe
siječe  u
u  i
i 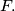 Dužina
Dužina  siječe kružnicu promjera
siječe kružnicu promjera  u
u 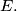 Kružnica sa središtem u
Kružnica sa središtem u  i polumjerom
i polumjerom 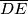 siječe
siječe  u
u  i
i 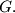 Odredi kut
Odredi kut 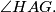 Odgovor treba napisati u stupnjevima, i treba napisati samo broj (dakle ako je odgovor
Odgovor treba napisati u stupnjevima, i treba napisati samo broj (dakle ako je odgovor 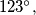 treba upisati samo 123).
treba upisati samo 123).
 radijusa
radijusa  sa središtem u
sa središtem u  te točka
te točka  na kružnici. Neka je
na kružnici. Neka je  polovište dužine
polovište dužine  i neka okomica na
i neka okomica na  u
u  siječe
siječe  u
u  i
i 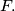 Dužina
Dužina  siječe kružnicu promjera
siječe kružnicu promjera  u
u 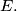 Kružnica sa središtem u
Kružnica sa središtem u  i polumjerom
i polumjerom 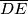 siječe
siječe  u
u  i
i 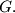 Odredi kut
Odredi kut 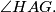 Odgovor treba napisati u stupnjevima, i treba napisati samo broj (dakle ako je odgovor
Odgovor treba napisati u stupnjevima, i treba napisati samo broj (dakle ako je odgovor 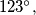 treba upisati samo 123).
treba upisati samo 123). Given a circle  with a radius of
with a radius of  centered at
centered at  and a point
and a point  on the circle. Let
on the circle. Let  be the midpoint of the segment
be the midpoint of the segment  , and let a perpendicular to
, and let a perpendicular to  at
at  intersect
intersect  at points
at points  and
and  . The segment
. The segment  intersects the circle with diameter
intersects the circle with diameter  at point
at point  . The circle centered at
. The circle centered at  with radius
with radius 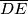 intersects
intersects  at points
at points  and
and  . Determine the angle
. Determine the angle 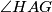 . The answer should be written in degrees, and only the number should be provided (so if the answer is
. The answer should be written in degrees, and only the number should be provided (so if the answer is 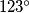 , you should just write 123).
, you should just write 123).
 with a radius of
with a radius of  centered at
centered at  and a point
and a point  on the circle. Let
on the circle. Let  be the midpoint of the segment
be the midpoint of the segment  , and let a perpendicular to
, and let a perpendicular to  at
at  intersect
intersect  at points
at points  and
and  . The segment
. The segment  intersects the circle with diameter
intersects the circle with diameter  at point
at point  . The circle centered at
. The circle centered at  with radius
with radius 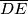 intersects
intersects  at points
at points  and
and  . Determine the angle
. Determine the angle 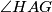 . The answer should be written in degrees, and only the number should be provided (so if the answer is
. The answer should be written in degrees, and only the number should be provided (so if the answer is 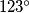 , you should just write 123).
, you should just write 123). 