Vrijeme: 05:32
Konstruktivne kritike | Constructive criticism #3
Ponovno je dana kružnica  radijusa
radijusa  sa središtem u
sa središtem u  i točka
i točka  na kružnici. Sada definirajmo
na kružnici. Sada definirajmo 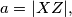 gdje su
gdje su  i
i  definirane kao u prvom zadatku ovog lanca. Na sličan način, definirajmo
definirane kao u prvom zadatku ovog lanca. Na sličan način, definirajmo 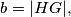 gdje su
gdje su  i
i  definirane kao u drugom zadatku ovog lanca. Sada se vratimo na našu kružnicu
definirane kao u drugom zadatku ovog lanca. Sada se vratimo na našu kružnicu  u ovom zadatku, i neka je
u ovom zadatku, i neka je  na
na  takva da je
takva da je 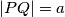 i da je
i da je 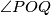 tup. Nadalje, neka je
tup. Nadalje, neka je  na
na  takva da je
takva da je 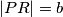 i takva da su
i takva da su  i
i  s iste strane pravca
s iste strane pravca 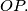 Naposlijetku, neka je
Naposlijetku, neka je 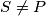 na
na  takva da je
takva da je 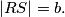 Odredi kut
Odredi kut 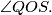 Odgovor treba napisati u stupnjevima, i treba napisati samo broj (dakle ako je odgovor
Odgovor treba napisati u stupnjevima, i treba napisati samo broj (dakle ako je odgovor 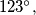 treba upisati samo 123).
treba upisati samo 123).
 radijusa
radijusa  sa središtem u
sa središtem u  i točka
i točka  na kružnici. Sada definirajmo
na kružnici. Sada definirajmo 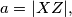 gdje su
gdje su  i
i  definirane kao u prvom zadatku ovog lanca. Na sličan način, definirajmo
definirane kao u prvom zadatku ovog lanca. Na sličan način, definirajmo 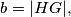 gdje su
gdje su  i
i  definirane kao u drugom zadatku ovog lanca. Sada se vratimo na našu kružnicu
definirane kao u drugom zadatku ovog lanca. Sada se vratimo na našu kružnicu  u ovom zadatku, i neka je
u ovom zadatku, i neka je  na
na  takva da je
takva da je 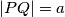 i da je
i da je 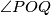 tup. Nadalje, neka je
tup. Nadalje, neka je  na
na  takva da je
takva da je 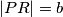 i takva da su
i takva da su  i
i  s iste strane pravca
s iste strane pravca 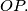 Naposlijetku, neka je
Naposlijetku, neka je 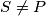 na
na  takva da je
takva da je 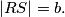 Odredi kut
Odredi kut 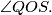 Odgovor treba napisati u stupnjevima, i treba napisati samo broj (dakle ako je odgovor
Odgovor treba napisati u stupnjevima, i treba napisati samo broj (dakle ako je odgovor 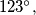 treba upisati samo 123).
treba upisati samo 123). Again, consider a circle  with a radius of
with a radius of  centered at
centered at  and a point
and a point  on the circle. Now, define
on the circle. Now, define 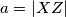 , where
, where  and
and  are defined as in the first problem of this chain. Similarly, define
are defined as in the first problem of this chain. Similarly, define 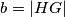 , where
, where  and
and  are defined as in the second problem of this chain. Now, return to our circle
are defined as in the second problem of this chain. Now, return to our circle  in this problem, and let
in this problem, and let  be a point on
be a point on  such that
such that 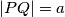 and
and 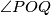 is obtuse. Furthermore, let
is obtuse. Furthermore, let  be a point on
be a point on  such that
such that 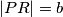 and that
and that  and
and  are on the same side of the line
are on the same side of the line 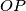 . Finally, let
. Finally, let 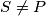 be a point on
be a point on  such that
such that 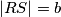 . Determine the angle
. Determine the angle 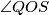 . The answer should be written in degrees, and only the number should be provided (so if the answer is
. The answer should be written in degrees, and only the number should be provided (so if the answer is 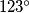 , you should just write 123).
, you should just write 123).
 with a radius of
with a radius of  centered at
centered at  and a point
and a point  on the circle. Now, define
on the circle. Now, define 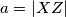 , where
, where  and
and  are defined as in the first problem of this chain. Similarly, define
are defined as in the first problem of this chain. Similarly, define 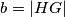 , where
, where  and
and  are defined as in the second problem of this chain. Now, return to our circle
are defined as in the second problem of this chain. Now, return to our circle  in this problem, and let
in this problem, and let  be a point on
be a point on  such that
such that 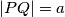 and
and 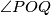 is obtuse. Furthermore, let
is obtuse. Furthermore, let  be a point on
be a point on  such that
such that 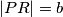 and that
and that  and
and  are on the same side of the line
are on the same side of the line 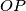 . Finally, let
. Finally, let 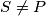 be a point on
be a point on  such that
such that 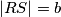 . Determine the angle
. Determine the angle 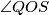 . The answer should be written in degrees, and only the number should be provided (so if the answer is
. The answer should be written in degrees, and only the number should be provided (so if the answer is 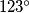 , you should just write 123).
, you should just write 123). 