Neka je
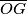
dužina duljine 4 i neka je

kružnica sa središtem u

i radijusom 2. Neka je točka

takva da je
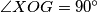
i
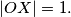
Neka su
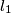
i
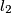
redom unutarnja i vanjska simetrala kuta
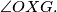
Neka
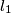
i
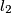
sijeku pravac

u

i
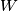
redom. Kružnica sa središtem u

i polumjerom
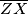
siječe pravac

u

i
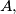
tako da je
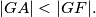
Kružnica sa središtem u
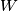
i polumjerom
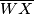
siječe pravac

u

i
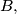
tako da je
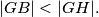
Neka je

takva da je
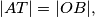
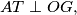
te su

i

s iste strane pravca
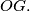
Neka kružnica promjera
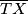
siječe pravac

u točkama

i
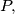
tako da je
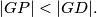
Neka okomica na

u

siječe

u točkama

i
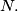
Odredi kut
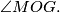
Budući da znamo da ste prethodna 3 zadatka mogli trivijalno nacrati i izmjeriti u geogebri, u želji da izbjegnemo takvo ponašanje i ovdje, ovog puta vas tražimo sljedeće: traženi 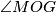 želimo zapisati u stupnjevima, u decimalnom zapisu (dakle ne želimo minute i sekunde, nego decimalni broj, npr. želimo
želimo zapisati u stupnjevima, u decimalnom zapisu (dakle ne želimo minute i sekunde, nego decimalni broj, npr. želimo 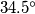 a ne
a ne 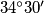 ) i želimo da kao odgovor napišete znamenke od 81. do 96. (uključivo) decimalnog mjesta (počinjemo brojati nakon decimalne točke, dakle u broju 76.542, znamenka 5 je na prvom mjestu, 4 je na drugom mjestu i 2 je na trećem mjestu). Dakle, vaš odgovor mora biti tih 16 znamenki, zapisane kao jedan 16-teroznamenkasti broj.
) i želimo da kao odgovor napišete znamenke od 81. do 96. (uključivo) decimalnog mjesta (počinjemo brojati nakon decimalne točke, dakle u broju 76.542, znamenka 5 je na prvom mjestu, 4 je na drugom mjestu i 2 je na trećem mjestu). Dakle, vaš odgovor mora biti tih 16 znamenki, zapisane kao jedan 16-teroznamenkasti broj.
Let
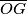
be a segment of length 4, and let

be a circle centered at

with a radius of 2. Let point

be such that
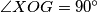
and
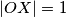
. Let
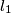
and
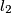
be the internal and external angle bisectors of angle
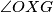
, respectively. Let
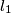
and
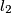
intersect line

at points

and
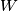
, respectively. The circle centered at

with radius
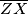
intersects line

at points

and

, such that
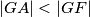
. The circle centered at
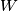
with radius
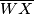
intersects line

at points

and

, such that
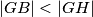
. Let

be such that
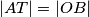
,
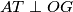
, and points

and

are on the same side of line

. The circle with diameter
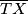
intersects line

at points

and

, such that
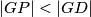
. A perpendicular to

at

intersects

at points

and

. Determine the angle
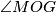
.
Since we know that you could easily draw and measure the previous three problems using GeoGebra, in order to avoid such behavior here, this time we ask you the following: we want the requested angle 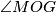 to be expressed in degrees, in decimal form (meaning we do not want minutes and seconds, but a decimal number, e.g., we want
to be expressed in degrees, in decimal form (meaning we do not want minutes and seconds, but a decimal number, e.g., we want 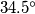 and not
and not 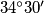 ). We also want you to provide the digits from the 81st to the 96th (inclusive) decimal place (starting to count after the decimal point, so in the number 76.542, the digit 5 is in the first position, 4 is in the second position, and 2 is in the third position). Therefore, your answer must consist of those 16 digits, written as a single 16-digit number.
). We also want you to provide the digits from the 81st to the 96th (inclusive) decimal place (starting to count after the decimal point, so in the number 76.542, the digit 5 is in the first position, 4 is in the second position, and 2 is in the third position). Therefore, your answer must consist of those 16 digits, written as a single 16-digit number.
[lang=hr]
Neka je $\overline{OG}$ dužina duljine 4 i neka je $\sigma$ kružnica sa središtem u $O$ i radijusom 2. Neka je točka $X$ takva da je $\angle XOG=90^\circ$ i $|OX|=1.$ Neka su $l_1$ i $l_2$ redom unutarnja i vanjska simetrala kuta $\angle OXG.$ Neka $l_1$ i $l_2$ sijeku pravac $OG$ u $Z$ i $W$ redom. Kružnica sa središtem u $Z$ i polumjerom $\overline{ZX}$ siječe pravac $OG$ u $F$ i $A,$ tako da je $|GA|<|GF|.$ Kružnica sa središtem u $W$ i polumjerom $\overline{WX}$ siječe pravac $OG$ u $H$ i $B,$ tako da je $|GB|<|GH|.$ Neka je $T$ takva da je $|AT|=|OB|,$ $AT \perp OG,$ te su $T$ i $X$ s iste strane pravca $OG.$ Neka kružnica promjera $\overline{TX}$ siječe pravac $OG$ u točkama $D$ i $P,$ tako da je $|GP|<|GD|.$ Neka okomica na $OG$ u $P$ siječe $\sigma$ u točkama $M$ i $N.$ Odredi kut $\angle MOG.$
Budući da znamo da ste prethodna 3 zadatka mogli trivijalno nacrati i izmjeriti u geogebri, u želji da izbjegnemo takvo ponašanje i ovdje, ovog puta vas tražimo sljedeće: traženi $\angle MOG$ želimo zapisati u stupnjevima, u decimalnom zapisu (dakle ne želimo minute i sekunde, nego decimalni broj, npr. želimo $34.5^\circ$ a ne $34^\circ 30'$) i želimo da kao odgovor napišete znamenke od 81. do 96. (uključivo) decimalnog mjesta (počinjemo brojati nakon decimalne točke, dakle u broju 76.542, znamenka 5 je na prvom mjestu, 4 je na drugom mjestu i 2 je na trećem mjestu). Dakle, vaš odgovor mora biti tih 16 znamenki, zapisane kao jedan 16-teroznamenkasti broj.
[/lang]
[lang=en]
Let $\overline{OG}$ be a segment of length 4, and let $\sigma$ be a circle centered at $O$ with a radius of 2. Let point $X$ be such that $\angle XOG=90^\circ$ and $|OX|=1$. Let $l_1$ and $l_2$ be the internal and external angle bisectors of angle $\angle OXG$, respectively. Let $l_1$ and $l_2$ intersect line $OG$ at points $Z$ and $W$, respectively. The circle centered at $Z$ with radius $\overline{ZX}$ intersects line $OG$ at points $F$ and $A$, such that $|GA|<|GF|$. The circle centered at $W$ with radius $\overline{WX}$ intersects line $OG$ at points $H$ and $B$, such that $|GB|<|GH|$. Let $T$ be such that $|AT|=|OB|$, $AT \perp OG$, and points $T$ and $X$ are on the same side of line $OG$. The circle with diameter $\overline{TX}$ intersects line $OG$ at points $D$ and $P$, such that $|GP|<|GD|$. A perpendicular to $OG$ at $P$ intersects $\sigma$ at points $M$ and $N$. Determine the angle $\angle MOG$.
Since we know that you could easily draw and measure the previous three problems using GeoGebra, in order to avoid such behavior here, this time we ask you the following: we want the requested angle $\angle MOG$ to be expressed in degrees, in decimal form (meaning we do not want minutes and seconds, but a decimal number, e.g., we want $34.5^\circ$ and not $34^\circ 30'$). We also want you to provide the digits from the 81st to the 96th (inclusive) decimal place (starting to count after the decimal point, so in the number 76.542, the digit 5 is in the first position, 4 is in the second position, and 2 is in the third position). Therefore, your answer must consist of those 16 digits, written as a single 16-digit number.
[/lang]
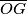 dužina duljine 4 i neka je
dužina duljine 4 i neka je  kružnica sa središtem u
kružnica sa središtem u  i radijusom 2. Neka je točka
i radijusom 2. Neka je točka  takva da je
takva da je 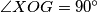 i
i 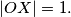 Neka su
Neka su 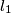 i
i 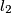 redom unutarnja i vanjska simetrala kuta
redom unutarnja i vanjska simetrala kuta 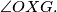 Neka
Neka 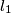 i
i 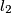 sijeku pravac
sijeku pravac  u
u  i
i 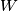 redom. Kružnica sa središtem u
redom. Kružnica sa središtem u  i polumjerom
i polumjerom 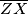 siječe pravac
siječe pravac  u
u  i
i 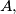 tako da je
tako da je 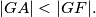 Kružnica sa središtem u
Kružnica sa središtem u 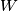 i polumjerom
i polumjerom 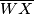 siječe pravac
siječe pravac  u
u  i
i 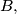 tako da je
tako da je 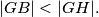 Neka je
Neka je  takva da je
takva da je 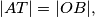
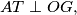 te su
te su  i
i  s iste strane pravca
s iste strane pravca 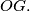 Neka kružnica promjera
Neka kružnica promjera 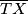 siječe pravac
siječe pravac  u točkama
u točkama  i
i 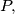 tako da je
tako da je 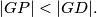 Neka okomica na
Neka okomica na  u
u  siječe
siječe  u točkama
u točkama  i
i 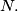 Odredi kut
Odredi kut 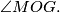
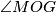 želimo zapisati u stupnjevima, u decimalnom zapisu (dakle ne želimo minute i sekunde, nego decimalni broj, npr. želimo
želimo zapisati u stupnjevima, u decimalnom zapisu (dakle ne želimo minute i sekunde, nego decimalni broj, npr. želimo 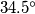 a ne
a ne 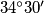 ) i želimo da kao odgovor napišete znamenke od 81. do 96. (uključivo) decimalnog mjesta (počinjemo brojati nakon decimalne točke, dakle u broju 76.542, znamenka 5 je na prvom mjestu, 4 je na drugom mjestu i 2 je na trećem mjestu). Dakle, vaš odgovor mora biti tih 16 znamenki, zapisane kao jedan 16-teroznamenkasti broj.
) i želimo da kao odgovor napišete znamenke od 81. do 96. (uključivo) decimalnog mjesta (počinjemo brojati nakon decimalne točke, dakle u broju 76.542, znamenka 5 je na prvom mjestu, 4 je na drugom mjestu i 2 je na trećem mjestu). Dakle, vaš odgovor mora biti tih 16 znamenki, zapisane kao jedan 16-teroznamenkasti broj. 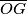 be a segment of length 4, and let
be a segment of length 4, and let  be a circle centered at
be a circle centered at  with a radius of 2. Let point
with a radius of 2. Let point  be such that
be such that 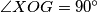 and
and 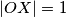 . Let
. Let 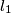 and
and 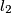 be the internal and external angle bisectors of angle
be the internal and external angle bisectors of angle 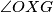 , respectively. Let
, respectively. Let 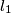 and
and 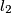 intersect line
intersect line  at points
at points  and
and 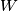 , respectively. The circle centered at
, respectively. The circle centered at  with radius
with radius 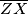 intersects line
intersects line  at points
at points  and
and  , such that
, such that 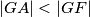 . The circle centered at
. The circle centered at 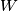 with radius
with radius 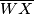 intersects line
intersects line  at points
at points  and
and  , such that
, such that 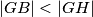 . Let
. Let  be such that
be such that 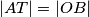 ,
, 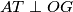 , and points
, and points  and
and  are on the same side of line
are on the same side of line  . The circle with diameter
. The circle with diameter 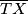 intersects line
intersects line  at points
at points  and
and  , such that
, such that 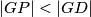 . A perpendicular to
. A perpendicular to  at
at  intersects
intersects  at points
at points  and
and  . Determine the angle
. Determine the angle 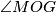 .
.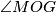 to be expressed in degrees, in decimal form (meaning we do not want minutes and seconds, but a decimal number, e.g., we want
to be expressed in degrees, in decimal form (meaning we do not want minutes and seconds, but a decimal number, e.g., we want 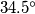 and not
and not 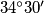 ). We also want you to provide the digits from the 81st to the 96th (inclusive) decimal place (starting to count after the decimal point, so in the number 76.542, the digit 5 is in the first position, 4 is in the second position, and 2 is in the third position). Therefore, your answer must consist of those 16 digits, written as a single 16-digit number.
). We also want you to provide the digits from the 81st to the 96th (inclusive) decimal place (starting to count after the decimal point, so in the number 76.542, the digit 5 is in the first position, 4 is in the second position, and 2 is in the third position). Therefore, your answer must consist of those 16 digits, written as a single 16-digit number. 