Neka je

polinom s cjelobrojnim koeficijentima za koji vrijedi
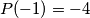
,
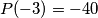
,
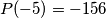
. Za koliko najviše brojeva vrijedi
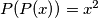
.
Let

be a polynomial with integer coefficients such that
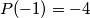
,
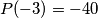
, and
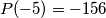
. What is the maximum number of solutions to the equation
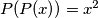
?
[lang=hr]
Neka je $P(x)$ polinom s cjelobrojnim koeficijentima za koji vrijedi $P(-1)=-4$, $P(-3)=-40$, $P(-5)=-156$. Za koliko najviše brojeva vrijedi $P(P(x))=x^2$.
[/lang]
[lang=en]
Let $P(x)$ be a polynomial with integer coefficients such that $P(-1) = -4$, $P(-3) = -40$, and $P(-5) = -156$. What is the maximum number of solutions to the equation $P(P(x)) = x^2$?
[/lang]