Vrijeme: 05:30
Boris is my name, geometry is my game | Boris is my name, geometry is my game #2
U trokutu  vrijedi
vrijedi 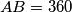 ,
, 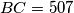 ,
, 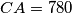 . Neka je
. Neka je  polovište stranice
polovište stranice  ,
,  točka na
točka na  tako da je
tako da je  simetrala
simetrala  . Neka je
. Neka je  točka na
točka na  takva da je
takva da je 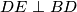 . Neka je
. Neka je 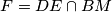 . Nađi
. Nađi 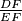 . Odgovor zaokruži na
. Odgovor zaokruži na  decimale.
decimale.
 vrijedi
vrijedi 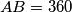 ,
, 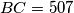 ,
, 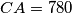 . Neka je
. Neka je  polovište stranice
polovište stranice  ,
,  točka na
točka na  tako da je
tako da je  simetrala
simetrala  . Neka je
. Neka je  točka na
točka na  takva da je
takva da je 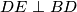 . Neka je
. Neka je 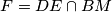 . Nađi
. Nađi 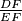 . Odgovor zaokruži na
. Odgovor zaokruži na  decimale.
decimale. In  ,
, 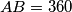 ,
, 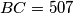 , and
, and 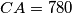 . Let
. Let  be the midpoint of
be the midpoint of  , and let
, and let  be the point on
be the point on  such that
such that  bisects angle
bisects angle  . Let
. Let  be the point on
be the point on  such that
such that 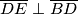 . Suppose that
. Suppose that 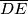 meets
meets 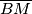 at
at  . Find
. Find 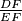 and round your solution to
and round your solution to  decimal places.
decimal places.
 ,
, 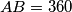 ,
, 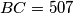 , and
, and 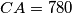 . Let
. Let  be the midpoint of
be the midpoint of  , and let
, and let  be the point on
be the point on  such that
such that  bisects angle
bisects angle  . Let
. Let  be the point on
be the point on  such that
such that 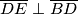 . Suppose that
. Suppose that 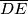 meets
meets 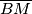 at
at  . Find
. Find 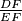 and round your solution to
and round your solution to  decimal places.
decimal places. 