Vrijeme: 05:30
Boris is my name, geometry is my game | Boris is my name, geometry is my game #5
Neka je  raznostranični trokut. Njemu upisana kružnica dodiruje stranice
raznostranični trokut. Njemu upisana kružnica dodiruje stranice  ,
,  i
i  u točkama
u točkama  ,
,  i
i  redom. Pripisana kružnica nasuprot vrha
redom. Pripisana kružnica nasuprot vrha  dodiruje pravce
dodiruje pravce  ,
,  i
i  u točkama
u točkama 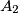 ,
, 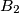 i
i  , respektivno. Pretpostavimo da se pravci
, respektivno. Pretpostavimo da se pravci 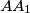 ,
, 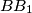 , and
, and 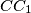 sijeku u točki
sijeku u točki  i da se pravci
i da se pravci 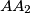 ,
, 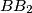 , and
, and 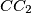 sijeku u točki
sijeku u točki 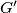 .Pravac
.Pravac 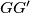 siječe unutarnju simetralu kuta
siječe unutarnju simetralu kuta  u točki
u točki  . Pretpostavimo da je
. Pretpostavimo da je 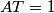 ,
, 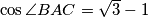 i da je
i da je ![BC=8\sqrt[4]{3}](/media/m/6/d/a/6da270833cac12cdbe8e99b612dcc3c0.png) . Nađi
. Nađi 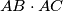 . Odgovor zaokruži na
. Odgovor zaokruži na  decimale.
decimale.
 raznostranični trokut. Njemu upisana kružnica dodiruje stranice
raznostranični trokut. Njemu upisana kružnica dodiruje stranice  ,
,  i
i  u točkama
u točkama  ,
,  i
i  redom. Pripisana kružnica nasuprot vrha
redom. Pripisana kružnica nasuprot vrha  dodiruje pravce
dodiruje pravce  ,
,  i
i  u točkama
u točkama 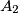 ,
, 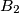 i
i  , respektivno. Pretpostavimo da se pravci
, respektivno. Pretpostavimo da se pravci 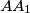 ,
, 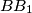 , and
, and 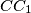 sijeku u točki
sijeku u točki  i da se pravci
i da se pravci 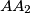 ,
, 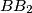 , and
, and 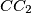 sijeku u točki
sijeku u točki 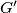 .Pravac
.Pravac 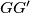 siječe unutarnju simetralu kuta
siječe unutarnju simetralu kuta  u točki
u točki  . Pretpostavimo da je
. Pretpostavimo da je 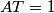 ,
, 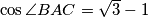 i da je
i da je ![BC=8\sqrt[4]{3}](/media/m/6/d/a/6da270833cac12cdbe8e99b612dcc3c0.png) . Nađi
. Nađi 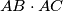 . Odgovor zaokruži na
. Odgovor zaokruži na  decimale.
decimale. Let  be a scalene triangle. The circle inscribed in it touches the sides
be a scalene triangle. The circle inscribed in it touches the sides  ,
,  and
and  at the points
at the points  ,
,  and
and  respectively. The escribed circle opposite to vertex
respectively. The escribed circle opposite to vertex  touches lines
touches lines  ,
,  , and
, and  at points
at points 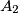 ,
, 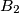 , and
, and  , respectively. Assume that lines
, respectively. Assume that lines 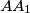 ,
, 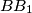 , and
, and 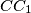 intersect at point
intersect at point  and that lines
and that lines 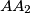 ,
, 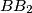 , and
, and 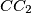 intersect at point
intersect at point 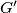 . Line
. Line 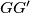 intersects the interior bisector of angle
intersects the interior bisector of angle  at point
at point  . Assume that
. Assume that 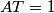 ,
, 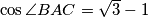 and that
and that ![BC=8\sqrt[4]{3}](/media/m/6/d/a/6da270833cac12cdbe8e99b612dcc3c0.png) . Find
. Find 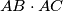 . Round the answer to 4 decimal places.
. Round the answer to 4 decimal places.
 be a scalene triangle. The circle inscribed in it touches the sides
be a scalene triangle. The circle inscribed in it touches the sides  ,
,  and
and  at the points
at the points  ,
,  and
and  respectively. The escribed circle opposite to vertex
respectively. The escribed circle opposite to vertex  touches lines
touches lines  ,
,  , and
, and  at points
at points 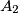 ,
, 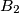 , and
, and  , respectively. Assume that lines
, respectively. Assume that lines 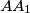 ,
, 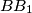 , and
, and 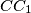 intersect at point
intersect at point  and that lines
and that lines 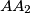 ,
, 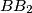 , and
, and 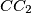 intersect at point
intersect at point 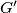 . Line
. Line 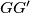 intersects the interior bisector of angle
intersects the interior bisector of angle  at point
at point  . Assume that
. Assume that 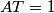 ,
, 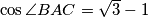 and that
and that ![BC=8\sqrt[4]{3}](/media/m/6/d/a/6da270833cac12cdbe8e99b612dcc3c0.png) . Find
. Find 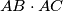 . Round the answer to 4 decimal places.
. Round the answer to 4 decimal places. 