Nažalost, Fran nije dobro izračunao koliko

treba biti (on je samo pretpostavio da treba biti
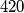
, pa šta bude, bude) pa ga je agent policijske postaje Vrbani III., Hank Šredović priveo u postaju. Na sreću po našeg prijatelja Frana, Sale zna da prema ustavu Neovisne Republike Vrbani, Fran ima pravo igrati igru s Hankom i ako ga Hank ne pobjedi, mora biti pušten na slobodu. Igra ide ovako:
Na stolu se nalazi 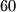 praznih kutija
praznih kutija 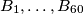 poslaganih u redu i beskonačna zaliha kamenčića te je zadan prirodni broj
poslaganih u redu i beskonačna zaliha kamenčića te je zadan prirodni broj  . U prvom krugu, Fran uzima
. U prvom krugu, Fran uzima  kamenčića i rasporedi ih u kutije kako god želi. Svaki idući krug se sastoji od dva koraka:
kamenčića i rasporedi ih u kutije kako god želi. Svaki idući krug se sastoji od dva koraka:
(a) Hank odabire prirodni  t.d.
t.d. 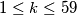 i podijeli kutije u dvije grupe
i podijeli kutije u dvije grupe 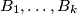 i
i 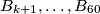 .
.
(b) Fran odabire jednu od te dvije grupe, dodaje jedan kamenčić u svaku kutije iz te grupe te ulanja po jedan kamenčić iz svake kutije druge grupe.
Hank pobjeđuje, ako na kraju nekog kruga, postoji kutija bez kamenčića. Nakon igre, Fran je sretno izašao iz zatvora. Koliki je najmanji  ?
?
Unfortunately, Fran didn’t calculate

correctly (he just guessed that it should be
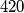
and hoped for the best), so he was arrested by Officer Hank Schrader of the Vrbani III. police station. Luckily for our friend Fran, Sale knows that according to the constitution of the Independent Republic of Vrbani, Fran has the right to play a game with Hank, and if Hank doesn’t win, Fran must be released. The game goes like this:
On the table, there are 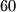 empty boxes
empty boxes 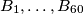 arranged in a row, and an infinite supply of pebbles. A natural number
arranged in a row, and an infinite supply of pebbles. A natural number  is also given. In the first round, Fran takes
is also given. In the first round, Fran takes  pebbles and distributes them among the boxes however he wishes. Each subsequent round consists of two steps:
pebbles and distributes them among the boxes however he wishes. Each subsequent round consists of two steps:
(a) Hank chooses a natural number  such that
such that 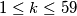 and divides the boxes into two groups:
and divides the boxes into two groups: 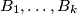 and
and 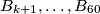 .
.
(b) Fran selects one of these two groups, adds one pebble to each box in that group, and removes one pebble from each box in the other group.
Hank wins if, at the end of any round, there is a box without any pebbles. After the game, Fran happily walked out of jail. What is the smallest  ?
?
[lang=hr]
Nažalost, Fran nije dobro izračunao koliko $T$ treba biti (on je samo pretpostavio da treba biti $420$, pa šta bude, bude) pa ga je agent policijske postaje Vrbani III., Hank Šredović priveo u postaju. Na sreću po našeg prijatelja Frana, Sale zna da prema ustavu Neovisne Republike Vrbani, Fran ima pravo igrati igru s Hankom i ako ga Hank ne pobjedi, mora biti pušten na slobodu. Igra ide ovako:
Na stolu se nalazi $60$ praznih kutija $B_1,\ldots,B_{60}$ poslaganih u redu i beskonačna zaliha kamenčića te je zadan prirodni broj $n$. U prvom krugu, Fran uzima $n$ kamenčića i rasporedi ih u kutije kako god želi. Svaki idući krug se sastoji od dva koraka: \\
(a) Hank odabire prirodni $k$ t.d. $1\leq k\leq 59$ i podijeli kutije u dvije grupe $B_1,\ldots,B_k$ i $B_{k+1},\ldots,B_{60}$.\\
(b) Fran odabire jednu od te dvije grupe, dodaje jedan kamenčić u svaku kutije iz te grupe te ulanja po jedan kamenčić iz svake kutije druge grupe.\\
Hank pobjeđuje, ako na kraju nekog kruga, postoji kutija bez kamenčića. Nakon igre, Fran je sretno izašao iz zatvora. Koliki je najmanji $n$?
[/lang]
[lang=en]
Unfortunately, Fran didn’t calculate $T$ correctly (he just guessed that it should be $420$ and hoped for the best), so he was arrested by Officer Hank Schrader of the Vrbani III. police station. Luckily for our friend Fran, Sale knows that according to the constitution of the Independent Republic of Vrbani, Fran has the right to play a game with Hank, and if Hank doesn’t win, Fran must be released. The game goes like this:
On the table, there are $60$ empty boxes $B_1,\ldots,B_{60}$ arranged in a row, and an infinite supply of pebbles. A natural number $n$ is also given. In the first round, Fran takes $n$ pebbles and distributes them among the boxes however he wishes. Each subsequent round consists of two steps: \\
(a) Hank chooses a natural number $k$ such that $1 \leq k \leq 59$ and divides the boxes into two groups: $B_1,\ldots,B_k$ and $B_{k+1},\ldots,B_{60}$. \\
(b) Fran selects one of these two groups, adds one pebble to each box in that group, and removes one pebble from each box in the other group. \\
Hank wins if, at the end of any round, there is a box without any pebbles. After the game, Fran happily walked out of jail. What is the smallest $n$?
[/lang]
 treba biti (on je samo pretpostavio da treba biti
treba biti (on je samo pretpostavio da treba biti 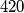 , pa šta bude, bude) pa ga je agent policijske postaje Vrbani III., Hank Šredović priveo u postaju. Na sreću po našeg prijatelja Frana, Sale zna da prema ustavu Neovisne Republike Vrbani, Fran ima pravo igrati igru s Hankom i ako ga Hank ne pobjedi, mora biti pušten na slobodu. Igra ide ovako:
, pa šta bude, bude) pa ga je agent policijske postaje Vrbani III., Hank Šredović priveo u postaju. Na sreću po našeg prijatelja Frana, Sale zna da prema ustavu Neovisne Republike Vrbani, Fran ima pravo igrati igru s Hankom i ako ga Hank ne pobjedi, mora biti pušten na slobodu. Igra ide ovako: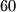 praznih kutija
praznih kutija 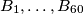 poslaganih u redu i beskonačna zaliha kamenčića te je zadan prirodni broj
poslaganih u redu i beskonačna zaliha kamenčića te je zadan prirodni broj  . U prvom krugu, Fran uzima
. U prvom krugu, Fran uzima  kamenčića i rasporedi ih u kutije kako god želi. Svaki idući krug se sastoji od dva koraka:
kamenčića i rasporedi ih u kutije kako god želi. Svaki idući krug se sastoji od dva koraka:  t.d.
t.d. 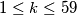 i podijeli kutije u dvije grupe
i podijeli kutije u dvije grupe 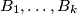 i
i 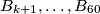 .
. ?
?  correctly (he just guessed that it should be
correctly (he just guessed that it should be 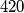 and hoped for the best), so he was arrested by Officer Hank Schrader of the Vrbani III. police station. Luckily for our friend Fran, Sale knows that according to the constitution of the Independent Republic of Vrbani, Fran has the right to play a game with Hank, and if Hank doesn’t win, Fran must be released. The game goes like this:
and hoped for the best), so he was arrested by Officer Hank Schrader of the Vrbani III. police station. Luckily for our friend Fran, Sale knows that according to the constitution of the Independent Republic of Vrbani, Fran has the right to play a game with Hank, and if Hank doesn’t win, Fran must be released. The game goes like this: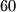 empty boxes
empty boxes 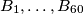 arranged in a row, and an infinite supply of pebbles. A natural number
arranged in a row, and an infinite supply of pebbles. A natural number  is also given. In the first round, Fran takes
is also given. In the first round, Fran takes  pebbles and distributes them among the boxes however he wishes. Each subsequent round consists of two steps:
pebbles and distributes them among the boxes however he wishes. Each subsequent round consists of two steps:  such that
such that 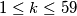 and divides the boxes into two groups:
and divides the boxes into two groups: 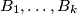 and
and 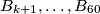 .
.  ?
? 