Vrijeme: 05:30
Demo G | Demo G #4
Zadan je trokut  . Neka su
. Neka su  i
i  točke na stranici
točke na stranici  takve da vrijedi
takve da vrijedi 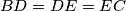 . Neka je
. Neka je  polovište stranice
polovište stranice  . Pravac
. Pravac 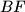 siječe
siječe  u točki
u točki  , a
, a  u točki
u točki  . Odredite omjer površine trokuta
. Odredite omjer površine trokuta 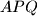 i četverokuta
i četverokuta 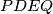 . Napišite odgovor u obliku razlomka poput
. Napišite odgovor u obliku razlomka poput 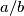 .
.
 . Neka su
. Neka su  i
i  točke na stranici
točke na stranici  takve da vrijedi
takve da vrijedi 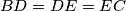 . Neka je
. Neka je  polovište stranice
polovište stranice  . Pravac
. Pravac 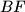 siječe
siječe  u točki
u točki  , a
, a  u točki
u točki  . Odredite omjer površine trokuta
. Odredite omjer površine trokuta 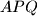 i četverokuta
i četverokuta 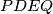 . Napišite odgovor u obliku razlomka poput
. Napišite odgovor u obliku razlomka poput 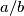 .
. Let  be a triangle. Let
be a triangle. Let 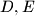 be points on the segment
be points on the segment  such that
such that 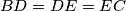 . Let
. Let  be the mid-point of
be the mid-point of  . Let
. Let 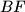 intersect
intersect  in
in  and
and  in
in  respectively. Determine the ratio of the area of the triangle
respectively. Determine the ratio of the area of the triangle 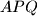 to that of the quadrilateral
to that of the quadrilateral 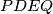 . Write the answer in fraction form like a/b.
. Write the answer in fraction form like a/b.
 be a triangle. Let
be a triangle. Let 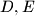 be points on the segment
be points on the segment  such that
such that 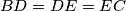 . Let
. Let  be the mid-point of
be the mid-point of  . Let
. Let 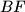 intersect
intersect  in
in  and
and  in
in  respectively. Determine the ratio of the area of the triangle
respectively. Determine the ratio of the area of the triangle 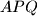 to that of the quadrilateral
to that of the quadrilateral 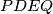 . Write the answer in fraction form like a/b.
. Write the answer in fraction form like a/b. 