Vrijeme: 05:31
Demo G | Demo G #3
U pravokutni trokut  s duljinom kateta
s duljinom kateta  i
i  , upisan je kvadrat
, upisan je kvadrat 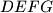 s dva susjedna vrha
s dva susjedna vrha  ,
,  na hipotenuzi
na hipotenuzi  (tako da je
(tako da je  bliže
bliže  ) i po jednim vrhom
) i po jednim vrhom  i
i  na katetama
na katetama  i
i  . Izračunajte
. Izračunajte  .
.
 s duljinom kateta
s duljinom kateta  i
i  , upisan je kvadrat
, upisan je kvadrat 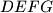 s dva susjedna vrha
s dva susjedna vrha  ,
,  na hipotenuzi
na hipotenuzi  (tako da je
(tako da je  bliže
bliže  ) i po jednim vrhom
) i po jednim vrhom  i
i  na katetama
na katetama  i
i  . Izračunajte
. Izračunajte  .
. In a right triangle  with legs of lengths
with legs of lengths  and
and  , a square
, a square 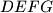 is inscribed such that two consecutive vertices
is inscribed such that two consecutive vertices  and
and  lie on the hypotenuse
lie on the hypotenuse  (so that
(so that  is closer to
is closer to  ), and the other two vertices
), and the other two vertices  and
and  lie on the legs
lie on the legs  and
and  , respectively. Calculate
, respectively. Calculate  .
.
 with legs of lengths
with legs of lengths  and
and  , a square
, a square 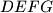 is inscribed such that two consecutive vertices
is inscribed such that two consecutive vertices  and
and  lie on the hypotenuse
lie on the hypotenuse  (so that
(so that  is closer to
is closer to  ), and the other two vertices
), and the other two vertices  and
and  lie on the legs
lie on the legs  and
and  , respectively. Calculate
, respectively. Calculate  .
. 