Odredite
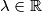
tako da je volumen paralelepipeda razapetog vektorima
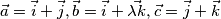
jednak 2. Rješenja odvojite zarezom, uzlazno sortrano.
Determine
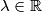
such that the volume of the parallelepiped spanned by the vectors
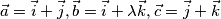
is equal to 2. Provide the solutions separated by commas, sorted in ascending order.
[lang=hr]
Odredite $\lambda \in \mathbb{R}$ tako da je volumen paralelepipeda razapetog vektorima $\vec{a}=\vec{i}+\vec{j}, \vec{b}=\vec{i}+\vec{ \lambda k}, \vec{c}=\vec{j}+\vec{k}$ jednak 2.
Rješenja odvojite zarezom, uzlazno sortrano.
[/lang]
[lang=en]
Determine $\lambda \in \mathbb{R}$ such that the volume of the parallelepiped spanned by the vectors $\vec{a}=\vec{i} + \vec{j}, \vec{b}=\vec{i} + \lambda \vec{k}, \vec{c}=\vec{j} + \vec{k}$ is equal to 2.
Provide the solutions separated by commas, sorted in ascending order.
[/lang]