Vrijeme: 05:33
Gravitacija pada | Gravity falls #4
Zvijezde  i
i  gibaju se oko središta masa po kružnim stazama polumjera
gibaju se oko središta masa po kružnim stazama polumjera 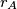 i
i 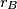 . Opažanjem je ustanovljeno da je razdoblje ophoda zvijezda oko zajedničkoga središta masa
. Opažanjem je ustanovljeno da je razdoblje ophoda zvijezda oko zajedničkoga središta masa  godina dok je uzajamna udaljenost zvijezda
godina dok je uzajamna udaljenost zvijezda 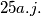 . Također, zvijezda
. Također, zvijezda  je 5 puta udaljenija od središta masa sustava nego zvijezda
je 5 puta udaljenija od središta masa sustava nego zvijezda  . Masa svijezde
. Masa svijezde  može se zapisati u obliku
može se zapisati u obliku 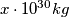 . Odredite
. Odredite  i zaokružite na dvije decimale. (
i zaokružite na dvije decimale. (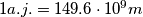 ,
, 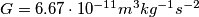 ,
, 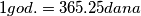 )
)
 i
i  gibaju se oko središta masa po kružnim stazama polumjera
gibaju se oko središta masa po kružnim stazama polumjera 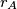 i
i 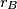 . Opažanjem je ustanovljeno da je razdoblje ophoda zvijezda oko zajedničkoga središta masa
. Opažanjem je ustanovljeno da je razdoblje ophoda zvijezda oko zajedničkoga središta masa  godina dok je uzajamna udaljenost zvijezda
godina dok je uzajamna udaljenost zvijezda 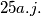 . Također, zvijezda
. Također, zvijezda  je 5 puta udaljenija od središta masa sustava nego zvijezda
je 5 puta udaljenija od središta masa sustava nego zvijezda  . Masa svijezde
. Masa svijezde  može se zapisati u obliku
može se zapisati u obliku 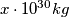 . Odredite
. Odredite  i zaokružite na dvije decimale. (
i zaokružite na dvije decimale. (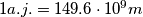 ,
, 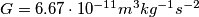 ,
, 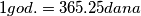 )
) Stars  and
and  move in circular orbits around their center of mass with radii
move in circular orbits around their center of mass with radii 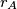 and
and 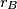 . Observations have shown that the orbital period of the stars around the common center of mass is
. Observations have shown that the orbital period of the stars around the common center of mass is  years, while the mutual distance between the stars is
years, while the mutual distance between the stars is 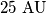 . Additionally, star
. Additionally, star  is 5 times farther from the center of mass of the system than star
is 5 times farther from the center of mass of the system than star  . The mass of star
. The mass of star  can be written in the form
can be written in the form 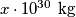 . Determine
. Determine  and round it to two decimals. (
and round it to two decimals. (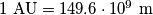 ,
, 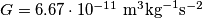 ,
, 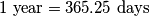 )
)
 and
and  move in circular orbits around their center of mass with radii
move in circular orbits around their center of mass with radii 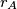 and
and 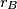 . Observations have shown that the orbital period of the stars around the common center of mass is
. Observations have shown that the orbital period of the stars around the common center of mass is  years, while the mutual distance between the stars is
years, while the mutual distance between the stars is 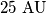 . Additionally, star
. Additionally, star  is 5 times farther from the center of mass of the system than star
is 5 times farther from the center of mass of the system than star  . The mass of star
. The mass of star  can be written in the form
can be written in the form 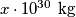 . Determine
. Determine  and round it to two decimals. (
and round it to two decimals. (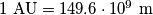 ,
, 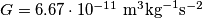 ,
, 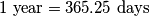 )
) 