Dani su vektori
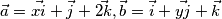
,
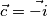
. Odredite
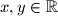
takve da su udaljenosti vektora
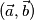
,
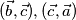
redom
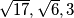
.
Given the vectors
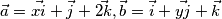
,
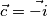
, determine
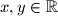
such that the distances between the vectors
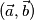
,
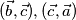
are
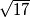
,
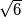
, and

, respectively.
[lang=hr]
Dani su vektori $\vec{a}=\vec{xi}+\vec{j}+\vec{2k}, \vec{b}=\vec{i}+\vec{yj}+\vec{k}$, $\vec{c}=\vec{-i} $.
Odredite $x, y \in \mathbb{R}$ takve da su udaljenosti vektora $(\vec{a}, \vec{b})$, $(\vec{b}, \vec{c}), (\vec{c}, \vec{a})$ redom $\sqrt {17}, \sqrt{6}, 3$.
[/lang]
[lang=en]
Given the vectors $\vec{a}=\vec{xi}+\vec{j}+\vec{2k}, \vec{b}=\vec{i}+\vec{yj}+\vec{k}$, $ \vec{c}=\vec{-i} $, determine $x, y \in \mathbb{R}$ such that the distances between the vectors $(\vec{a}, \vec{b})$, $(\vec{b}, \vec{c}), (\vec{c}, \vec{a})$ are $\sqrt{17}$, $\sqrt{6}$, and $3$, respectively.
[/lang]