Dobrodošli na Hrvojevu funkcijsku matematičku olimpijadu! Kao što ovo originalno ime govori, cijeli lanac se sastoji isključivo od funkcijskih jednadžbi. S obzirom da je zapisivanje funkcija kao rješenja na ovom natjecanju malo komplicirano, ovaj prvi zadatak služi vama kao uputa za predavanje rješenja. Recimo da su rješenja neke funkcijske jednadžbe
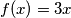
,
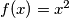
i
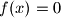
. Rješenje zapišite na način da iterirate

-eve od

do

uključno. Za

navedena rješenja daju rješenja

,

i

. Zapišite te brojeve sortirano uzlazno i odvojene zarezom ("0,1,3"). Zatim isto napravite za
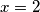
(sada vam rješenje treba izgledati kao "0,1,3,0,4,6"). I tako sve do

uključno. Pokušajte sami napisati to rješenje i unesite ga u polje za rješenje ovog konkretnog zadatka kako biste mogli nastaviti dalje s lancem. Imate

pokušaja.
Welcome to Hrvoje's Functional Mathematics Olympiad!
As the name suggests, the entire chain of problems consists solely of functional equations. Since expressing functions as solutions in this competition can be a bit tricky, this first problem serves as a guide for how to submit your solutions.
Let’s say the solutions to a given functional equation are 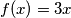 ,
, 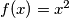 , and
, and 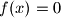 . You need to present the solution by iterating the values of
. You need to present the solution by iterating the values of  from
from  to
to  , inclusive. For
, inclusive. For  , the given functions produce the values
, the given functions produce the values  ,
,  , and
, and  . Write these values in ascending order, separated by commas (like "0,1,3"). Then, do the same for
. Write these values in ascending order, separated by commas (like "0,1,3"). Then, do the same for 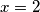 (your solution should now look like "0,1,3,0,4,6"). Continue this process for all values up to
(your solution should now look like "0,1,3,0,4,6"). Continue this process for all values up to  .
.
Try to write out the solution yourself and enter it in the answer field for this specific task so you can proceed further in the problem chain. You have  attempts.
attempts.
[lang=hr]
Dobrodošli na Hrvojevu funkcijsku matematičku olimpijadu!
Kao što ovo originalno ime govori, cijeli lanac se sastoji isključivo od funkcijskih jednadžbi.
S obzirom da je zapisivanje funkcija kao rješenja na ovom natjecanju malo komplicirano, ovaj prvi zadatak služi vama kao uputa za predavanje rješenja.
Recimo da su rješenja neke funkcijske jednadžbe $f(x) = 3x$, $f(x) = x^2$ i $f(x) = 0$. Rješenje zapišite na način da iterirate $x$ -eve od $1$ do $5$ uključno. Za $x=1$ navedena rješenja daju rješenja $3$, $1$ i $0$. Zapišite te brojeve sortirano uzlazno i odvojene zarezom ("0,1,3"). Zatim isto napravite za $x=2$ (sada vam rješenje treba izgledati kao "0,1,3,0,4,6"). I tako sve do $5$ uključno.
Pokušajte sami napisati to rješenje i unesite ga u polje za rješenje ovog konkretnog zadatka kako biste mogli nastaviti dalje s lancem. Imate $10$ pokušaja.
[/lang]
[lang=en]
Welcome to Hrvoje's Functional Mathematics Olympiad!
As the name suggests, the entire chain of problems consists solely of functional equations. Since expressing functions as solutions in this competition can be a bit tricky, this first problem serves as a guide for how to submit your solutions.
Let’s say the solutions to a given functional equation are $f(x) = 3x$, $f(x) = x^2$, and $f(x) = 0$. You need to present the solution by iterating the values of $x$ from $1$ to $5$, inclusive. For $x=1$, the given functions produce the values $3$, $1$, and $0$. Write these values in ascending order, separated by commas (like "0,1,3"). Then, do the same for $x=2$ (your solution should now look like "0,1,3,0,4,6"). Continue this process for all values up to $5$.
Try to write out the solution yourself and enter it in the answer field for this specific task so you can proceed further in the problem chain. You have $10$ attempts.
[/lang]
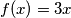 ,
, 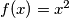 i
i 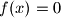 . Rješenje zapišite na način da iterirate
. Rješenje zapišite na način da iterirate  -eve od
-eve od  do
do  uključno. Za
uključno. Za  navedena rješenja daju rješenja
navedena rješenja daju rješenja  ,
,  i
i  . Zapišite te brojeve sortirano uzlazno i odvojene zarezom ("0,1,3"). Zatim isto napravite za
. Zapišite te brojeve sortirano uzlazno i odvojene zarezom ("0,1,3"). Zatim isto napravite za 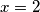 (sada vam rješenje treba izgledati kao "0,1,3,0,4,6"). I tako sve do
(sada vam rješenje treba izgledati kao "0,1,3,0,4,6"). I tako sve do  uključno. Pokušajte sami napisati to rješenje i unesite ga u polje za rješenje ovog konkretnog zadatka kako biste mogli nastaviti dalje s lancem. Imate
uključno. Pokušajte sami napisati to rješenje i unesite ga u polje za rješenje ovog konkretnog zadatka kako biste mogli nastaviti dalje s lancem. Imate  pokušaja.
pokušaja. 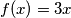 ,
, 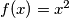 , and
, and 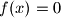 . You need to present the solution by iterating the values of
. You need to present the solution by iterating the values of  from
from  to
to  , inclusive. For
, inclusive. For  , the given functions produce the values
, the given functions produce the values  ,
,  , and
, and  . Write these values in ascending order, separated by commas (like "0,1,3"). Then, do the same for
. Write these values in ascending order, separated by commas (like "0,1,3"). Then, do the same for 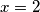 (your solution should now look like "0,1,3,0,4,6"). Continue this process for all values up to
(your solution should now look like "0,1,3,0,4,6"). Continue this process for all values up to  .
. attempts.
attempts. 