Neka je
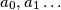
jedinstveni niz cijelih brojeva za koje je:
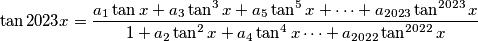
kad god je lijeva strana definirana. Nađite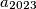 
Here's the translated math problem in English:
Let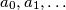 
be a unique sequence of integers such that:
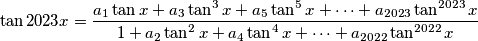
whenever the left side is defined. Find .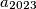
[lang=hr]
Neka je $a_0, a_1 \dots$ jedinstveni niz cijelih brojeva za koje je:
$$
\tan2023x = \frac{a_1 \tan x + a_3 \tan^3 x + a_5 \tan^5 x + \cdots + a_{2023} \tan^{2023} x}{1 + a_2 \tan^2 x + a_4 \tan^4 x \cdots + a_{2022} \tan^{2022} x}
$$
kad god je lijeva strana definirana. Nađite $a_{2023}$
[/lang]
[lang=en]
Here's the translated math problem in English:
Let $a_0, a_1, \dots$ be a unique sequence of integers such that:
$$
\tan2023x = \frac{a_1 \tan x + a_3 \tan^3 x + a_5 \tan^5 x + \cdots + a_{2023} \tan^{2023} x}{1 + a_2 \tan^2 x + a_4 \tan^4 x + \cdots + a_{2022} \tan^{2022} x}
$$
whenever the left side is defined. Find $a_{2023}$.
[/lang]
