Koeficijenti

polinoma
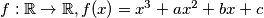
su međusobno različiti cijeli brojevi takvi da je
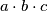
različito od

. Također vrijedi:
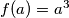
i
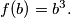
Odredi

.
The coefficients

of a polynomial
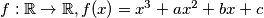
are mutually distinct integers and different from zero. Furthermore,
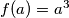
and
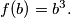
Determine

.
[lang=hr]
Koeficijenti $a,b,c$ polinoma $f:\mathbb{R}\to\mathbb{R}, f(x)=x^3+ax^2+bx+c$ su međusobno različiti cijeli brojevi takvi da je $a \cdot b \cdot c$ različito od $0$. Također vrijedi: $f(a)=a^3$ i $f(b)=b^3.$ Odredi $c$.
[/lang]
[lang=en]
The coefficients $a,b,c$ of a polynomial $f:\mathbb{R}\to\mathbb{R}, f(x)=x^3+ax^2+bx+c$ are mutually distinct integers and different from zero. Furthermore, $f(a)=a^3$ and $f(b)=b^3.$ Determine $c$.
[/lang]