Vrijeme: 05:33
Familija | Family #1
Zadane su točke 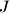 ,
,  ,
,  ,
,  i
i  . Točke
. Točke 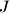 ,
,  ,
,  i
i  povezane čine paralelogram čija površina iznosi
povezane čine paralelogram čija površina iznosi  , a točka
, a točka  je takva da leži na polovištu dužine
je takva da leži na polovištu dužine 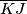 . Neka je
. Neka je 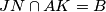 . Izračunajte površinu četverokuta
. Izračunajte površinu četverokuta 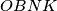 . Rješenje napišite kao decimalni broj zaokružen na tri decimale (npr. 5.171).
. Rješenje napišite kao decimalni broj zaokružen na tri decimale (npr. 5.171).
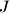 ,
,  ,
,  ,
,  i
i  . Točke
. Točke 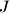 ,
,  ,
,  i
i  povezane čine paralelogram čija površina iznosi
povezane čine paralelogram čija površina iznosi  , a točka
, a točka  je takva da leži na polovištu dužine
je takva da leži na polovištu dužine 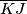 . Neka je
. Neka je 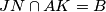 . Izračunajte površinu četverokuta
. Izračunajte površinu četverokuta 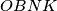 . Rješenje napišite kao decimalni broj zaokružen na tri decimale (npr. 5.171).
. Rješenje napišite kao decimalni broj zaokružen na tri decimale (npr. 5.171). Given the points 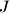 ,
,  ,
,  ,
,  and
and  . The points
. The points 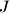 ,
,  ,
,  and
and  form a parallelogram with an area of
form a parallelogram with an area of  and the point
and the point  lies at the midpoint of the segment
lies at the midpoint of the segment 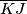 . Let
. Let 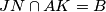 . Calculate the area of the quadrilateral
. Calculate the area of the quadrilateral 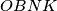 . Enter the solution as a decimal number rounded to three decimal places (e.g. 5.171).
. Enter the solution as a decimal number rounded to three decimal places (e.g. 5.171).
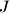 ,
,  ,
,  ,
,  and
and  . The points
. The points 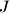 ,
,  ,
,  and
and  form a parallelogram with an area of
form a parallelogram with an area of  and the point
and the point  lies at the midpoint of the segment
lies at the midpoint of the segment 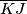 . Let
. Let 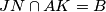 . Calculate the area of the quadrilateral
. Calculate the area of the quadrilateral 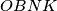 . Enter the solution as a decimal number rounded to three decimal places (e.g. 5.171).
. Enter the solution as a decimal number rounded to three decimal places (e.g. 5.171). 