Vrijeme: 06:58
Familija | Family #3
Dan je trokut 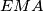 s ortocentrom
s ortocentrom  i središtem opisane kružnice
i središtem opisane kružnice  .
. 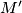 je presjek simetrale kuta
je presjek simetrale kuta 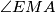 i opisane kružnice trokuta. Ako je
i opisane kružnice trokuta. Ako je 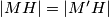 , odredi
, odredi 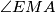 .
.
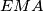 s ortocentrom
s ortocentrom  i središtem opisane kružnice
i središtem opisane kružnice  .
. 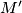 je presjek simetrale kuta
je presjek simetrale kuta 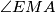 i opisane kružnice trokuta. Ako je
i opisane kružnice trokuta. Ako je 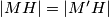 , odredi
, odredi 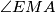 .
. Let 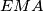 be a triangle with circumcircle
be a triangle with circumcircle  , and let
, and let  ,
,  be the triangle’s circumcenter and orthocenter respectively. Let also
be the triangle’s circumcenter and orthocenter respectively. Let also 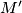 be the point where the angle bisector of the angle
be the point where the angle bisector of the angle 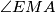 meets
meets  . If
. If 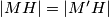 , then find the measure of the angle
, then find the measure of the angle 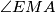 .
.
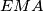 be a triangle with circumcircle
be a triangle with circumcircle  , and let
, and let  ,
,  be the triangle’s circumcenter and orthocenter respectively. Let also
be the triangle’s circumcenter and orthocenter respectively. Let also 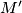 be the point where the angle bisector of the angle
be the point where the angle bisector of the angle 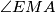 meets
meets  . If
. If 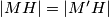 , then find the measure of the angle
, then find the measure of the angle 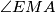 .
. 