Neka je
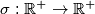
funkcija za koju vrijedi
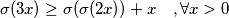
Odredite najveći
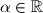
za koji vrijedi
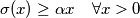
Let
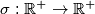
be a function such that:
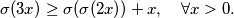
Determine the largest
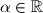
such that:
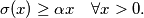
[lang=hr]
Neka je $\sigma: \mathbb{R}^+ \rightarrow \mathbb{R}^+$ funkcija za koju vrijedi
$$\sigma(3x) \geq \sigma(\sigma(2x)) + x \quad ,\forall x > 0$$
Odredite najveći $\alpha \in \mathbb{R}$ za koji vrijedi
$$\sigma(x) \geq \alpha x \quad \forall x > 0$$
[/lang]
[lang=en]
Let $\sigma: \mathbb{R}^+ \rightarrow \mathbb{R}^+$ be a function such that:
$$\sigma(3x) \geq \sigma(\sigma(2x)) + x, \quad \forall x > 0.$$
Determine the largest $\alpha \in \mathbb{R}$ such that:
$$\sigma(x) \geq \alpha x \quad \forall x > 0.$$
[/lang]