Marinada '24

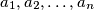[lang=hr] Nije FIFA kojoj se nadao, ali je fiFA koju je trebao. Neka je $N$ zbroj kvadrata svih prirodnih brojeva $n$ takvih da postoje prirodni brojevi $a_1,a_2, \ldots, a_n$ za koje vrijedi da skup 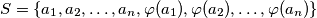$S = \{a_1, a_2, \ldots, a_n, \varphi(a_1), \varphi(a_2), \ldots, \varphi(a_n)\}$ sadrži točno $2n$ uzastopnih brojeva (u nekom odgovarajućem poretku elemenata skupa). Odredi $N$. [/lang] [lang=en] It's not the FIFA he hoped for, but it's the fiFA he needed. 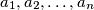Let $N$ be the sum of the squares of all natural numbers $n$ such that there exist natural numbers $a_1, a_2, \ldots, a_n$ for which the set 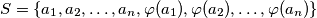$S = \{a_1, a_2, \ldots, a_n, \varphi(a_1), \varphi(a_2), \ldots, \varphi(a_n)\}$ contains exactly $2n$ consecutive numbers (in some appropriate order of the set's elements). Determine $N$. [/lang]