Vrijeme: 07:33
Fraktali | Fractals #2
Zadana je kružnica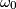 
u koju su upisane tri sukladne kružnice tako da su sve četiri kružnice međusobno tangentne. U dio ravnine između tri manje kružnice upisana je nova kružnica 
koja izvana dodiruje svaku od tih triju kružnica. Taj postupak upisivanja kružnica se nastavlja u beskonačnost. Ako je radijus kružnice 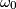jednak 
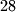, koliki je radijus kružnice 
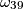? Rješenje upišite u znanstvenom zapisu s dvije decimale, sve bez razmaka (npr. 2.80*10^(-39)).
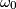u koju su upisane tri sukladne kružnice tako da su sve četiri kružnice međusobno tangentne. U dio ravnine između tri manje kružnice upisana je nova kružnica koja izvana dodiruje svaku od tih triju kružnica. Taj postupak upisivanja kružnica se nastavlja u beskonačnost. Ako je radijus kružnice 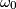jednak 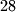, koliki je radijus kružnice 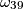? Rješenje upišite u znanstvenom zapisu s dvije decimale, sve bez razmaka (npr. 2.80*10^(-39)). A circle 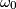is given, inside of which three congruent circles are inscribed, such that all four circles are mutually tangent. In the region of the plane between the three smaller circles, a new circle is inscribed, touching each of the three circles externally. This process of inscribing circles continues infinitely. 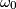If the radius of circle is 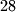, what is the radius of circle 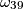? Write your answer in scientific notation with two decimal places, with no spaces (e.g. 2.80*10^(-39)).
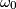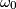is given, inside of which three congruent circles are inscribed, such that all four circles are mutually tangent. In the region of the plane between the three smaller circles, a new circle is inscribed, touching each of the three circles externally. This process of inscribing circles continues infinitely. If the radius of circle is 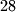, what is the radius of circle 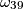? Write your answer in scientific notation with two decimal places, with no spaces (e.g. 2.80*10^(-39)).